题目内容
14. 已知E、F分别是正方形ABCD的边BC、DC上的点,且∠EAF=45°,自E、F分别作AC的垂线,垂足为P、Q,求证:AB2=AP•AQ.
已知E、F分别是正方形ABCD的边BC、DC上的点,且∠EAF=45°,自E、F分别作AC的垂线,垂足为P、Q,求证:AB2=AP•AQ.
分析 证得△ABE∽△AQF,得出$\frac{AB}{AQ}$=$\frac{AE}{AF}$,同理证得△AEP∽△AFD,得出$\frac{AE}{AF}$=$\frac{AP}{AD}$,代换整理求出结论即可.
解答 证明:如图,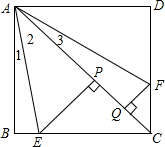
∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,∠BAC=45°=∠1+∠2,
∵∠EAF=45°=∠2+∠3,
∴∠1=∠3,
∵FQ⊥AC,
∴∠AQF=∠B=90°,
∴△ABE∽△AQF,
∴$\frac{AB}{AQ}$=$\frac{AE}{AF}$,
同理可得:△AEP∽△AFD,
∴$\frac{AE}{AF}$=$\frac{AP}{AD}$,
∴$\frac{AB}{AQ}$=$\frac{AP}{AD}$,
∴AB2=AP•AQ.
点评 本题考查了正方形性质,相似三角形的性质和判定,掌握三角形相似的判定方法是解决问题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,AM⊥BC于M,AN⊥CD于N.求证:AC•AM=MN•AB.
如图,在?ABCD中,AM⊥BC于M,AN⊥CD于N.求证:AC•AM=MN•AB.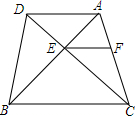 如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE.
如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).