题目内容
某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
X(元) | 3 | 4 | 5 | 6 |
y(个) | 20 | 15 | 12 | 10 |
(1)根据表中的数据在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为w元,试求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
(1)如下图,直接建立坐标系描点即可.
(2)y与x之间的函数关系式为:y= .
.

【解析】
(1)如下图,直接建立坐标系描点即可.
(2)如图所示:设函数关系式为y= (k≠0且k为常数),把点(3,20)代入y=
(k≠0且k为常数),把点(3,20)代入y= 中得,k=60,又将(4,15)(5,12)(6,10)分别代入,成立.所以y与x之间的函数关系式为:y=
中得,k=60,又将(4,15)(5,12)(6,10)分别代入,成立.所以y与x之间的函数关系式为:y= .
.

(3)∵ ,则w在x>0的范围内是随x的增大而增大,又∵x≤10,∴当x=10,W最大,∴此时获得最大日销
,则w在x>0的范围内是随x的增大而增大,又∵x≤10,∴当x=10,W最大,∴此时获得最大日销 售利润为48元.
售利润为48元.
【难度】一般

练习册系列答案
相关题目
 的图象经过(-1,-2).
的图象经过(-1,-2). )在这个函数图象上,求
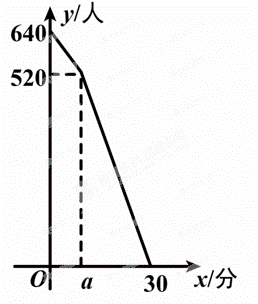
)在这个函数图象上,求 ,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分)之间的关系如图所示.
,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分)之间的关系如图所示.