题目内容
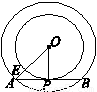
 如图所示.以O为圆心,半径为2的圆与反比例函数y=
如图所示.以O为圆心,半径为2的圆与反比例函数y=| k |
| x |
 |
| AB |
| 1 |
| 3 |
| 3 |
| 3 |
分析:连接OA、OB,由弧长公式求出∠AOB的度数,过点A作AC⊥x轴,过点B作BD⊥y轴,由于点AB均在反比例函数y=
的图象上,所以BD×OD=AC×OC=k,再由OB=OA可知,BD=AC,OD=OC,故△AOC≌△BOD,由此可求出∠AOC的度数,再设A(a,b),根据锐角三角函数的定义即可求出a、b的值.
| k |
| x |
解答: 解:连接OA、OB,
解:连接OA、OB,
∵
的长度为
π,OA=OB=2,
∴
=
π,解得n=30°,即∠AOB=30°,
过点A作AC⊥x轴,过点B作BD⊥y轴,
∵点AB均在反比例函数y=
的图象上,
∴BD×OD=AC×OC=k,
∵OB=OA,
∴BD=AC,OD=OC,
∴△AOC≌△BOD,
∴∠AOC=
=
=30°,
设A(a,b),则OC=OA•cos30°=2×
=
,AC=b=OA×sin30°=2×
=1,
∴k=ab=
×1=
.
故答案为:
.
 解:连接OA、OB,
解:连接OA、OB,∵
 |
| AB |
| 1 |
| 3 |
∴
| nπ×2 |
| 180 |
| 1 |
| 3 |
过点A作AC⊥x轴,过点B作BD⊥y轴,
∵点AB均在反比例函数y=
| k |
| x |
∴BD×OD=AC×OC=k,
∵OB=OA,
∴BD=AC,OD=OC,
∴△AOC≌△BOD,
∴∠AOC=
| 90°-∠AOB |
| 2 |
| 90°-30° |
| 2 |
设A(a,b),则OC=OA•cos30°=2×
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴k=ab=
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题考查的是反比例函数综合题,根据题意作出辅助线构造出直角三角形,再根据反比例函数系数k的几何意义进行解答即可.

练习册系列答案
相关题目
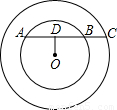
 14、如图所示,以O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于C,若AB=3,BC=1,则与圆环的面积最接近的整数是( )
14、如图所示,以O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于C,若AB=3,BC=1,则与圆环的面积最接近的整数是( ) 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦 是小圆的切线,点
是小圆的切线,点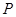 为切点,且
为切点,且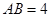 ,
,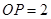 ,连结
,连结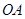 交小圆于点
交小圆于点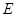 ,则扇形
,则扇形 的面积为 .
的面积为 .