题目内容
计算
(1)(4a3b-6a2b2+12ab3)÷(-2ab)
(2)(-x)3•x2n+x2n+1•(-x2)
(3)|-3|+(-1)2013×(π-3)0-(-
)-3.
(1)(4a3b-6a2b2+12ab3)÷(-2ab)
(2)(-x)3•x2n+x2n+1•(-x2)
(3)|-3|+(-1)2013×(π-3)0-(-
| 1 |
| 2 |
考点:整式的混合运算,零指数幂,负整数指数幂
专题:计算题
分析:(1)原式利用多项式除以单项式法则计算即可得到结果;
(2)原式利用单项式乘以单项式法则计算,合并即可得到结果;
(3)原式第一项利用绝对值的代数意义化简,第二项利用乘方的意义及零指数幂法则计算,最后一项利用负指数幂法则计算即可得到结果.
(2)原式利用单项式乘以单项式法则计算,合并即可得到结果;
(3)原式第一项利用绝对值的代数意义化简,第二项利用乘方的意义及零指数幂法则计算,最后一项利用负指数幂法则计算即可得到结果.
解答:解:(1)原式=-2a2+3ab-6b2;
(2)原式=-x2n+3-x2n+3=-2x2n+3;
(3)原式=3-1+8=10.
(2)原式=-x2n+3-x2n+3=-2x2n+3;
(3)原式=3-1+8=10.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
西安市2010年平均房价为每平方米5500元,连续两年增长后,2012年平均房价达到每平方米7000元.设这两年平均房价年增长率为x,根据题意,下面所列方程正确的是( )
| A、7000(1+x)2=5500 |
| B、7000(1-x)2=5500 |
| C、5500(1-x)2=7000 |
| D、5500(1+x)2=7000 |
AE,CF是锐角三角形ABC的两条高,如果AE:CF=3:2,则sin∠BAC:sin∠ACB等于( )
| A、3:2 | B、2:3 |
| C、9:4 | D、4:9 |
 有三张背面完全相同的卡片上分别写有一个整式,把它们背面朝上洗匀,小明从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张,第一次抽取的卡片上的整式做分子,第二次抽取的卡片上的整式做分母,则能组成分式的概率是
有三张背面完全相同的卡片上分别写有一个整式,把它们背面朝上洗匀,小明从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张,第一次抽取的卡片上的整式做分子,第二次抽取的卡片上的整式做分母,则能组成分式的概率是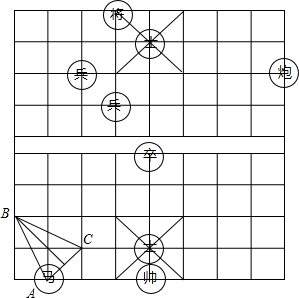 亲爱的同学,你会玩中国象棋吗?如图所示的一盘象棋中.马走的两步棋从A到B再到C,若小正方形边长为1,求B到AC的距离.
亲爱的同学,你会玩中国象棋吗?如图所示的一盘象棋中.马走的两步棋从A到B再到C,若小正方形边长为1,求B到AC的距离.