题目内容
12.如图,为了确定一条河的宽度,测量人员在对岸岸边P点处观察到一根柱子,再在他们所在的这一侧岸上选点A和点B,使得B,A,P在同一条直线上,且与河岸垂直,随后确定点C,点D,使BC⊥BP,AD⊥BP,由观测可以确定CP与AD的交点D.他们测得AB=45m,BC=90m,AD=60m,从而确定河宽,他们测量的河宽为90 m.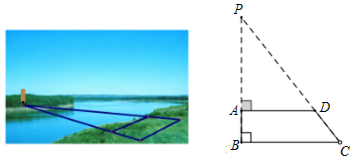
分析 证出△PAD和△PBC相似,然后根据相似三角形对应边成比例列式求解即可.
解答 解:∵BC⊥BP,AD⊥BP,
∴AD∥BC,
∴△PAD∽△PBC,
∴$\frac{AD}{BC}$=$\frac{PA}{PB}$,即$\frac{60}{90}$=$\frac{PA}{PA+45}$,
解得:PA=90.
故答案为:90.
点评 本题考查了相似三角形的应用,利用相似三角形对应边成比例列出比例式是解题的关键.

练习册系列答案
相关题目
 如图,一条船从灯塔C的南偏东42°的A处出发,向正北航行8海里到达B处,此时灯塔C在船的北偏西84°方向,则船距离灯塔C8海里.
如图,一条船从灯塔C的南偏东42°的A处出发,向正北航行8海里到达B处,此时灯塔C在船的北偏西84°方向,则船距离灯塔C8海里.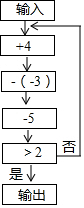 如图是一个数值转换机,输入数值后按三个方框中的程序运算,若第一次运算结果大于2,可以输出结果,则称该数只要“算一遍”;若第一次运算无法输出结果,且第二次运算结果大于2,可以输出结果,则称该数需要“算两遍”,以此类推:
如图是一个数值转换机,输入数值后按三个方框中的程序运算,若第一次运算结果大于2,可以输出结果,则称该数只要“算一遍”;若第一次运算无法输出结果,且第二次运算结果大于2,可以输出结果,则称该数需要“算两遍”,以此类推: