题目内容
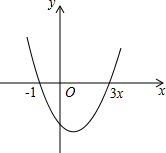 已知函数y=x2-2x-3的图象如图所示.
已知函数y=x2-2x-3的图象如图所示.(1)作图关于x轴对称,得到的图象的函数解析式是
(2)作图关于y轴对称,得到的图象的函数解析式是
(3)作图关于原点对称,得到的图象的函数解析式是
(4)把图象绕定点旋转180°,得到的图象的函数解析式是
考点:二次函数图象与几何变换
专题:几何变换
分析:把y=x2-2x-3配成顶点式得到y=(x-1)2-4,则抛物线的顶点坐标为(1,-4),
(1)根据关于x轴对称的点的坐标特征得到变换后的顶点坐标为(1,4),且抛物线开口方向相反,然后根据顶点式写出解析式;
(2)根据关于y轴对称的点的坐标特征得到变换后的顶点坐标为(-1,-4),然后根据顶点式写出解析式;
(3)根据关于原点对称的点的坐标特征得到变换后的顶点坐标为(-1,4),且抛物线开口方向相反,然后根据顶点式写出解析式;
(4)由于图象绕定点旋转180°,得到顶点坐标不变,而抛物线开口方向相反,然后根据顶点式写出解析式.
(1)根据关于x轴对称的点的坐标特征得到变换后的顶点坐标为(1,4),且抛物线开口方向相反,然后根据顶点式写出解析式;
(2)根据关于y轴对称的点的坐标特征得到变换后的顶点坐标为(-1,-4),然后根据顶点式写出解析式;
(3)根据关于原点对称的点的坐标特征得到变换后的顶点坐标为(-1,4),且抛物线开口方向相反,然后根据顶点式写出解析式;
(4)由于图象绕定点旋转180°,得到顶点坐标不变,而抛物线开口方向相反,然后根据顶点式写出解析式.
解答:解:y=x2-2x-3=(x-1)2-4,抛物线的顶点坐标为(1,-4),
(1)作图关于x轴对称,由于(1,-4)关于x轴的对称点为(1,4),且抛物线开口方向相反,所以得到的图象的函数解析式是y=-(x-1)2+4=-x2+2x+3;
(2)作图关于y轴对称,由于(1,-4)关于y轴的对称点为(-1,-4),所以得到的图象的函数解析式是y=(x+1)2-4=x2+2x-3;
(3)作图关于原点对称,由于(1,-4)关于原点的对称点为(-1,4),且抛物线开口方向相反,所以得到的图象的函数解析式是y=-(x+1)2+4=-x2-2x+3;
(4)把图象绕定点旋转180°,顶点坐标不变,而抛物线开口方向相反,所以得到的图象的函数解析式是y=-(x-1)2-4=-x2+2x-5.
故答案为y=-x2+2x+3;y=x2+2x-3;y=-x2-2x+3;y=-x2+2x-5.
(1)作图关于x轴对称,由于(1,-4)关于x轴的对称点为(1,4),且抛物线开口方向相反,所以得到的图象的函数解析式是y=-(x-1)2+4=-x2+2x+3;
(2)作图关于y轴对称,由于(1,-4)关于y轴的对称点为(-1,-4),所以得到的图象的函数解析式是y=(x+1)2-4=x2+2x-3;
(3)作图关于原点对称,由于(1,-4)关于原点的对称点为(-1,4),且抛物线开口方向相反,所以得到的图象的函数解析式是y=-(x+1)2+4=-x2-2x+3;
(4)把图象绕定点旋转180°,顶点坐标不变,而抛物线开口方向相反,所以得到的图象的函数解析式是y=-(x-1)2-4=-x2+2x-5.
故答案为y=-x2+2x+3;y=x2+2x-3;y=-x2-2x+3;y=-x2+2x-5.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
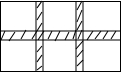 如图是宽为30m,长为44m的矩形草皮,要修筑同样宽的三条水渠(两条纵向,一条横向,且互相垂直),把草皮分成六块,要使余下草皮的面积为1120m2,求水渠宽为多少米?
如图是宽为30m,长为44m的矩形草皮,要修筑同样宽的三条水渠(两条纵向,一条横向,且互相垂直),把草皮分成六块,要使余下草皮的面积为1120m2,求水渠宽为多少米?