题目内容
在四边形ABCD与四边形A′B′C′D′中，AB=3，BC=5，∠D=50°，A′B′=6，要使四边形ABCD∽四边形A′B′C′D′，则B′C′= ，∠B′= °．
考点：相似多边形的性质
专题：计算题
分析：根据相似多边形的性质求解．
解答：解：∵四边形ABCD∽四边形A′B′C′D′，
∴
=
，即
=
，∠D′=∠D=50°．
∴B′C′=10．
故答案为10，50．
∴
| B′C′ |
| BC |
| A′B′ |
| AB |
| B′C′ |
| 5 |
| 6 |
| 3 |
∴B′C′=10．
故答案为10，50．
点评：本题考查了相似多边形的性质：如果两个多边形的对应角相等，对应边的比相等，则这两个多边形是相似多边形．相似多边形对应边的比叫做相似比．相似多边形的性质为：
对应角相等；对应边的比相等．
对应角相等；对应边的比相等．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
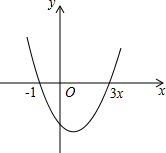已知函数y=x2-2x-3的图象如图所示．
如图，在△ABC中，∠A=45°，∠B=70°，则外角∠ACD=方程xy-x-y-2=0的整数解的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |