题目内容
2．
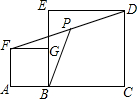如图，点A、B在一直线上，以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE，点P是DF的中点，连结BP．已知AB=3cm，BC=9cm，则BP的值是（ ）| A． | 6cm | B． | $\frac{3\sqrt{13}}{2}$cm | C． | 4$\sqrt{3}$cm | D． | 3$\sqrt{5}$cm |
分析 作PH∥CD交AC于H，根据梯形的中位线定理得到PH的值，根据正方形的性质得到BH的值，根据勾股定理得到答案．
解答 
解：作PH∥CD交AC于H，
∵CD∥AF，
∴CD∥AF，又点P是DF的中点，
∴点H是AC的中点，
∴PH=$\frac{1}{2}$（AF+CD）=6，AH=6，
BH=AH-AB=3，
∴BP=$\sqrt{B{H}^{2}+P{H}^{2}}$=3$\sqrt{5}$，
故选：D．
点评 本题考查的是梯形的中位线定理、正方形的性质和勾股定理的应用，掌握梯形的中位线平行于两底且等于两底和的一半是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
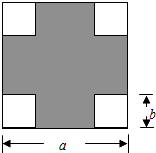如图，在一块边长为a的正方形纸板的四周，各剪去一个边长为b（b＜$\frac{a}{2}$）的正方形．
已知AD是∠BAC的平分线，EF⊥AD于P，交BC的延长线于M，求证：∠M=$\frac{1}{2}$（∠ACB-∠B）．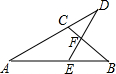
如图，在△ABC中，D是AC延长线上的一点，E是AB上的一点，连接DE交BC于点F，已知∠A=27°，∠EFB=85°，∠B=38°，求∠D和∠DEB的度数．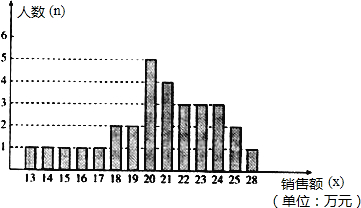
课外活动时，小明不小心将教室花架上的一块三角形玻璃打碎了，他看着地上的碎玻璃（如图）着急地说：“是我不小心打碎的．我想赶快去配一块，可玻璃已碎了，尺寸大小都不知道怎么办呢？”同学小灵说：“别急，只要你拿一块玻璃就可以去配上与原来完全相同的玻璃．”请想一想，应该拿哪一块呢？为什么？
11．
如图，若AB=AC，∠1=∠2，则下列条件不能使△ABD≌△ACE的是（ ）
如图，若AB=AC，∠1=∠2，则下列条件不能使△ABD≌△ACE的是（ ）| A． | AE=AD | B． | ∠B=∠C | C． | ∠E=∠D | D． | BD=CE |