题目内容
13. 已知AD是∠BAC的平分线,EF⊥AD于P,交BC的延长线于M,求证:∠M=$\frac{1}{2}$(∠ACB-∠B).
已知AD是∠BAC的平分线,EF⊥AD于P,交BC的延长线于M,求证:∠M=$\frac{1}{2}$(∠ACB-∠B).
分析 由角的互余关系得出∠M=90°-∠PDM,再由角平分线的定义、三角形的外角性质以及三角形内角和定理得出∠PDM=90°-$\frac{1}{2}$(∠ACB-∠B),即可得出结论.
解答 解:∵EF⊥AD,
∴∠MPD=90°,
∴∠M=90°-∠PDM,
∵AD是∠BAC的平分线,
∴∠BAD=$\frac{1}{2}$∠BAC,
∵∠PDM=∠BAD+∠B=$\frac{1}{2}$∠BAC+∠B,
∵∠BAC+∠B+∠ACB=180°,
∴2∠PDM=∠BAC+2∠B=180°-∠ACB+∠B,
∴∠PDM=90°-$\frac{1}{2}$(∠ACB-∠B),
∴∠M=$\frac{1}{2}$(∠ACB-∠B).
点评 本题考查了角平分线的定义、三角形的外角性质、三角形内角和定理;熟练掌握三角形内角和定理,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
2.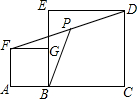 如图,点A、B在一直线上,以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE,点P是DF的中点,连结BP.已知AB=3cm,BC=9cm,则BP的值是( )
如图,点A、B在一直线上,以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE,点P是DF的中点,连结BP.已知AB=3cm,BC=9cm,则BP的值是( )
 如图,点A、B在一直线上,以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE,点P是DF的中点,连结BP.已知AB=3cm,BC=9cm,则BP的值是( )
如图,点A、B在一直线上,以AB、BC为边在同侧分别作正方形ABGF和正方形BCDE,点P是DF的中点,连结BP.已知AB=3cm,BC=9cm,则BP的值是( )| A. | 6cm | B. | $\frac{3\sqrt{13}}{2}$cm | C. | 4$\sqrt{3}$cm | D. | 3$\sqrt{5}$cm |

 如图,△ABC≌△ADE,∠1=70°,点E正好在线段BC上,求∠FEB和∠EAC.
如图,△ABC≌△ADE,∠1=70°,点E正好在线段BC上,求∠FEB和∠EAC. 如图,已知?ABCD中,∠AEF=∠ACB,AD=kAC,试判断AE、EF的数量关系.
如图,已知?ABCD中,∠AEF=∠ACB,AD=kAC,试判断AE、EF的数量关系.