题目内容
9.如图,小东将一张长AD为12、宽AB为4的矩形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P,Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置变化而发生改变.(1)请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
(2)如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
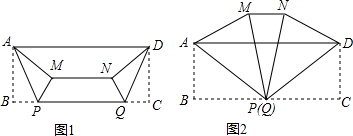
分析 (1)①根据矩形的性质得到∠B=∠C=90°,AB=CD.根据全等三角形的性质得到∠APB=∠DQG.推出△MEP≌△NPQ,由全等三角形的性质即可得到ME=NF;②根据矩形的判定定理得到四边形EFMN是矩形,由矩形的性质得到结论;
(2)证明△EMP∽△MAG,根据相似三角形的对应边的比相等,以及矩形的性质即可求解;
(3)设PM、PN分别交AD于点E、F,证明△PEF∽△PMN,根据相似三角形的对应边的比相等即可求解.
解答 解:(1)①∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD.
∵在△ABP和△DCQ中,
$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠C}\\{BP=CQ}\end{array}\right.$,
∴△ABP≌△DCQ,
∴∠APB=∠DQG.
∴∠MPE=180°-2∠APB=180°-2∠DQC=∠NQF.
∴在△MEP和△NPQ中,
$\left\{\begin{array}{l}{∠MPE=∠NQF}\\{∠MEP=∠NPQ}\\{MP=NQ}\end{array}\right.$,
∴△MEP≌△NPQ,
∴ME=NF;
②∵ME∥NF,ME=NF,
∴四边形EFMN是矩形,
∴MN∥BC;
(2)延长EM、FN交AD于点G、H,
∵AB=4,BP=3,
∴AM=4,PM=3.
∵AD∥BC,
∴EM⊥AD.
∵∠AMP=∠MEP=∠MGA,
∴∠EMP=∠MAG.
∴△EMP∽△MAG.
∴$\frac{AG}{EM}$=$\frac{MG}{EP}$=$\frac{AM}{MP}$=$\frac{4}{3}$,
设AG=4a,MG=3b.
∵四边形ABEG是矩形,
∴$\left\{\begin{array}{l}{4a=3b+3}\\{3a+4b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{24}{25}}\\{b=\frac{7}{25}}\end{array}\right.$,
∴AG=$\frac{96}{25}$,同理DH=$\frac{96}{25}$.
∴MN=$\frac{108}{25}$;
(3)设PM、PN分别交AD于点E、F.
∵∠EPA=∠APB=∠PAE,
∴EA=EP.
设EA=EP=x,
在直角△AME中,42+(6-x)2=x2,
解得:x=$\frac{13}{9}$,
∴EF=12-2×$\frac{13}{3}$=$\frac{10}{3}$,
∵EF∥MN,
∴△PEF∽△PMN,
∴$\frac{EF}{MN}$=$\frac{PE}{PM}$,即$\frac{\frac{10}{3}}{MN}=\frac{\frac{13}{3}}{6}$,
解得:MN=$\frac{60}{13}$.
点评 本题考查了图形的折叠,矩形的判定和性质,以及全等三角形的判定与性质和相似三角形的判定与性质,注意在求线段的长时常用的方法是利用相似和解直角三角形.

 名校课堂系列答案
名校课堂系列答案| A. | y=3(x-2)2+2 | B. | y=3(x+2)2-2 | C. | y=3(x-2)2+2 | D. | y=3(x+2)2+2 |
| A. | 30,27 | B. | 30,29 | C. | 29,30 | D. | 30,28 |

 如图,抛物线y=x2-mx-3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
如图,抛物线y=x2-mx-3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC. 小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)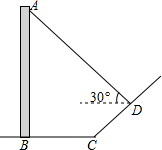 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)