题目内容
12. 一副直角三角板如图放置,点A在DF延长线上,BC∥DA,∠D=∠BAC=90°,∠E=30°,∠C=45°,AC=9$\sqrt{2}$
一副直角三角板如图放置,点A在DF延长线上,BC∥DA,∠D=∠BAC=90°,∠E=30°,∠C=45°,AC=9$\sqrt{2}$(1)求∠ABF的度数;
(2)若取$\sqrt{3}$=1.73,试求AF的长(计算结果保留两位小数)
分析 (1)先根据直角三角形两锐角互余求出∠DFE=90°-∠E=60°,∠ABC=∠C=45°,再利用平行线的性质得出∠CBF=∠DFE=60°,那么由∠ABF=∠CBF-∠ABC即可求出∠ABF的度数;
(2)过点B作BM⊥FD于点M,解直角△ACB,得出AB=AC=9$\sqrt{2}$,由BC∥DA,得到∠BAM=∠ABC=45°,那么AM=BM=$\frac{\sqrt{2}}{2}$AB=9.再解直角△BFM,求出FM=$\frac{BM}{tan60°}$=3$\sqrt{3}$,根据AF=AM-FM即可得出答案.
解答 解:(1)∵∠D=∠BAC=90°,∠E=30°,∠C=45°,
∴∠DFE=90°-∠E=60°,∠ABC=∠C=45°,
∵BC∥DA,
∴∠CBF=∠DFE=60°,
∴∠ABF=∠CBF-∠ABC=15°;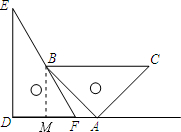 (2)过点B作BM⊥FD于点M,
(2)过点B作BM⊥FD于点M,
∵在△ACB中,∠BAC=90°,∠ABC=∠C=45°,AC=9$\sqrt{2}$,
∴AB=AC=9$\sqrt{2}$,
∵BC∥DA,
∴∠BAM=∠ABC=45°,
∴AM=BM=$\frac{\sqrt{2}}{2}$AB=9.
∵在△BFM中,∠BMF=90°,∠BFM=60°,
∴FM=$\frac{BM}{tan60°}$=3$\sqrt{3}$,
∴AF=AM-FM=9-3$\sqrt{3}$≈3.81.
点评 本题考查了解直角三角形,平行线的性质,锐角三角函数定义,难度中等,解答此类题目的关键根据题意建立三角形利用所学的三角函数的关系进行解答.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
14.利用平方根去根号可以构造一个整系数方程.例如:x=$\sqrt{2}$+1时,移项得x-1=$\sqrt{2}$,两边平方得(x-1)2=($\sqrt{2}$)2,所以x2-2x+1=2,即x2-2x-1=0.仿照上述构造方法,当x=$\frac{\sqrt{6}-1}{2}$时,可以构造出一个整系数方程是( )
| A. | 4x2+4x+5=0 | B. | 4x2+4x-5=0 | C. | x2+x+1=0 | D. | x2+x-1=0 |
3.已知△ABC中,∠A+∠B>∠C,则△ABC的形状是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 以上都不对 |
4.老王家的鱼塘中放养了某种鱼1500条,若干年后,准备打捞出售,为了估计鱼塘中这种鱼的总质量,现从鱼塘中捕捞三次,得到数据如下表:
(1)鱼塘中这种鱼平均每条重约多少千克?
(2)若这种鱼放养的成活率是82%,鱼塘中这种鱼约有多少千克?
(3)如果把这种鱼全部卖掉,价格为每千克6元,若投资成本为14000元,这种鱼的纯收入是多少元?
| 鱼的条数 | 平均每条鱼的质量/千克 | |
| 第1次 | 15 | 3.0 |
| 第2次 | 20 | 2.8 |
| 第3次 | 10 | 2.5 |
(2)若这种鱼放养的成活率是82%,鱼塘中这种鱼约有多少千克?
(3)如果把这种鱼全部卖掉,价格为每千克6元,若投资成本为14000元,这种鱼的纯收入是多少元?
 如图,在△ABC中,AB=AC,∠BAC=120°,AE=BE,D为EC中点.
如图,在△ABC中,AB=AC,∠BAC=120°,AE=BE,D为EC中点. 已知二次函数的图象经过点(0,-3),(2,5),(-1,-4)且与x轴交于A、B两点,其顶点为P.
已知二次函数的图象经过点(0,-3),(2,5),(-1,-4)且与x轴交于A、B两点,其顶点为P. 如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=40°,求∠C的度数.
如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=40°,求∠C的度数.