题目内容
 已知:如图,二次函数y=ax2+4的图象与x轴交于点A和点B(点A在点B 的左侧),与y轴交于点C,且cos∠CAO=
已知:如图,二次函数y=ax2+4的图象与x轴交于点A和点B(点A在点B 的左侧),与y轴交于点C,且cos∠CAO=
| ||
| 2 |
(1)求二次函数的解析式;
(2)若以点O为圆心的圆与直线AC相切于点D,求点D的坐标;
(3)在(2)的条件下,抛物线上是否存在点P使得以P、A、D、O为顶点的四边形是直角梯形?若存在,请求出点P坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:综合题
分析:(1)对于二次函数解析式,令x=0求出y的值确定出C坐标,根据题意得到三角形AOC为等腰直角三角形,确定出A坐标,代入二次函数解析式求出a的值,即可确定出解析式;
(2)连接OD,作DE∥y轴,交x轴于点E,DF∥x轴,交y轴于点F,如图1所示,由圆O与直线AC相切于点D,得到OD垂直于AC,由OA=OC,利用三线合一得到D为AC中点,进而求出DE与DF的长,确定出D坐标即可;
(3)分两种情况考虑:经过点A且与直线OD平行的直线的解析式为y=-x-4,与抛物线解析式联立求出P坐标;经过点O且与直线AC平行的直线的解析式为y=x,与抛物线解析式联立求出P坐标即可.
(2)连接OD,作DE∥y轴,交x轴于点E,DF∥x轴,交y轴于点F,如图1所示,由圆O与直线AC相切于点D,得到OD垂直于AC,由OA=OC,利用三线合一得到D为AC中点,进而求出DE与DF的长,确定出D坐标即可;
(3)分两种情况考虑:经过点A且与直线OD平行的直线的解析式为y=-x-4,与抛物线解析式联立求出P坐标;经过点O且与直线AC平行的直线的解析式为y=x,与抛物线解析式联立求出P坐标即可.
解答:解:(1)∵二次函数y=ax2+4的图象与y轴交于点C,
∴点C的坐标为(0,4),
∵二次函数y=ax2+4的图象与x轴交于点A,cos∠CAO=
,
∴∠CAO=45°,
∴OA=OC=4,
∴点A的坐标为(-4,0),
∴0=a(-4)2+4,
∴a=-
,
∴这二次函数的解析式为y=-
x2+4;
(2)连接OD,作DE∥y轴,交x轴于点E,DF∥x轴,交y轴于点F,如图1所示,
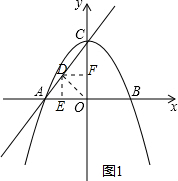
∵⊙O与直线AC相切于点D,
∴OD⊥AC,
∵OA=OC=4,
∴点D是AC的中点,
∴DE=
OC=2,DF=
OA=2,
∴点D的坐标为(-2,2);
(3)直线OD的解析式为y=-x,如图2所示,
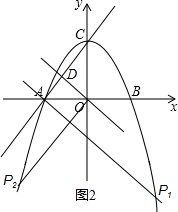
则经过点A且与直线OD平行的直线的解析式为y=-x-4,
解方程组
,
消去y,得x2-4x-32=0,即(x-8)(x+4)=0,
∴x1=8,x2=-4(舍去),
∴y=-12,
∴点P1的坐标为(8,-12);
直线AC的解析式为y=x+4,
则经过点O且与直线AC平行的直线的解析式为y=x,
解方程组
,
消去y,得x2+4x-16=0,即x=-2+2
,
∴x1=-2-2
,x2=-2+2
(舍去),
∴y=-2-2
,
∴点P2的坐标为(-2-2
,-2-2
).
∴点C的坐标为(0,4),
∵二次函数y=ax2+4的图象与x轴交于点A,cos∠CAO=
| ||
| 2 |
∴∠CAO=45°,
∴OA=OC=4,
∴点A的坐标为(-4,0),
∴0=a(-4)2+4,
∴a=-
| 1 |
| 4 |
∴这二次函数的解析式为y=-
| 1 |
| 4 |
(2)连接OD,作DE∥y轴,交x轴于点E,DF∥x轴,交y轴于点F,如图1所示,

∵⊙O与直线AC相切于点D,
∴OD⊥AC,
∵OA=OC=4,
∴点D是AC的中点,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴点D的坐标为(-2,2);
(3)直线OD的解析式为y=-x,如图2所示,

则经过点A且与直线OD平行的直线的解析式为y=-x-4,
解方程组
|
消去y,得x2-4x-32=0,即(x-8)(x+4)=0,
∴x1=8,x2=-4(舍去),
∴y=-12,
∴点P1的坐标为(8,-12);
直线AC的解析式为y=x+4,
则经过点O且与直线AC平行的直线的解析式为y=x,
解方程组
|
消去y,得x2+4x-16=0,即x=-2+2
| 5 |
∴x1=-2-2
| 5 |
| 5 |
∴y=-2-2
| 5 |
∴点P2的坐标为(-2-2
| 5 |
| 5 |
点评:此题属于二次函数综合题,涉及的知识有:待定系数法确定二次函数解析式,坐标与图形性质,直线与抛物线的交点,直线与圆相切的性质,锐角三角函数定义,以及等腰直角三角形的性质,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个正方形的面积是13,估计它的边长大小在( )
| A、2与3之间 |
| B、3与4之间 |
| C、4与5之间 |
| D、5与6之间 |
如果a>b,那么结论中错误的是( )
| A、a-4>b-4 | ||||
| B、4a>4b | ||||
C、
| ||||
| D、-a>-b |
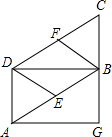 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点.
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点.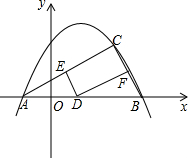 如图,已知抛物线y=-
如图,已知抛物线y=- 如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据:
如图所示,当小明站立在镜子EF前A处时,他看自己的脚在镜中的像的俯角为45°;如果小华向后退0.6米到B处,这时他看自己的脚在镜中的像的俯角为30°.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据: 某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下:
某市对九年级学生进行了一次学业水平测试,成绩评定分A、B、C、D四个等第.为了解这次数学测试成绩情况,相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析,相应数据的统计图表如下: 如图,已知直线PA:y=x+1交y轴于Q,直线PB:y=-2x+m.若四边形PQOB的面积为
如图,已知直线PA:y=x+1交y轴于Q,直线PB:y=-2x+m.若四边形PQOB的面积为