题目内容
E、F分别是∠AOB的两边OA、OB上的点,且OE=OF,OA=OB,AE、BF交于P.求证:OP平分∠AOB.(用两种方法)
考点:全等三角形的判定与性质
专题:证明题
分析:①先根据SAS证明△OAF≌△OBE,得出对应角相等,再根据AAS证明△APE≌△BPF,得出对应边相等,最后根据SSS证明△AOP≌△BOP,即可得出结论;
②先证明OP垂直平分AB,再根据等腰三角形的三线合一性质即可得出结论.
②先证明OP垂直平分AB,再根据等腰三角形的三线合一性质即可得出结论.
解答:
①证明:在△OAF和△OBE中,
,
∴△OAF≌△OBE(SAS),
∴∠OAF=∠OBE,
∵OE=OF,OA=OB,
∴AE=BF,
在△APE和△BPF中,
,
∴△APE≌△BPF(AAS),
∴PA=PB,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(SSS),
∴∠AOP=∠BOP,
∴OP平分∠AOB;
②证明:∵OA=OB,
∴O在AB的垂直平分线上,
由①得,PA=PB,
∴P在AB的垂直平分线上,
∴OP垂直平分AB,
∵OA=OB,
∴OP平分∠AOB(三线合一).
|
∴△OAF≌△OBE(SAS),
∴∠OAF=∠OBE,
∵OE=OF,OA=OB,
∴AE=BF,
在△APE和△BPF中,
|
∴△APE≌△BPF(AAS),
∴PA=PB,
在△AOP和△BOP中,
|
∴△AOP≌△BOP(SSS),
∴∠AOP=∠BOP,
∴OP平分∠AOB;
②证明:∵OA=OB,
∴O在AB的垂直平分线上,
由①得,PA=PB,
∴P在AB的垂直平分线上,
∴OP垂直平分AB,
∵OA=OB,
∴OP平分∠AOB(三线合一).
点评:本题考查了全等三角形的判定与性质以及线段垂直平分线的判定;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
下列是二元一次方程的是( )
| A、3x=10 |
| B、2x-3y=-1 |
| C、4x=y-z |
| D、xy+8=0 |
某人从A地步行到B地,当走到预定时间时,离B地还有0.5千米;若把步行速度提高25%,则可比预定时间早半小时到达B地.已知AB两地相距12.5千米,则某人原来步行的速度是( )
| A、2千米/时 |
| B、4千米/时 |
| C、5千米/时 |
| D、6千米/时 |
 如图,这是一个由小正方体搭成的几何体的俯视图,小正方形内的数字表示在该位置的小立方体的个数,请画出该几何体的主视图和左视图.
如图,这是一个由小正方体搭成的几何体的俯视图,小正方形内的数字表示在该位置的小立方体的个数,请画出该几何体的主视图和左视图.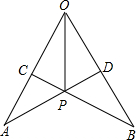 如图,∠AOP=∠BOP,AD⊥OB于D,BC⊥OA于C,AD与BC交于点P,求证:AP=BP.
如图,∠AOP=∠BOP,AD⊥OB于D,BC⊥OA于C,AD与BC交于点P,求证:AP=BP.