题目内容
 如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).(1)直接写出B点坐标;
(2)若过点C的直线CD交AB边于点D,且把矩形OABC的周长分为1:3两部分,求直线CD的解析式.
分析:(1)B的横坐标与A的横坐标相同,纵坐标与C的纵坐标相同.
(2)根据比例的性质求得BD的长,即可求得D的坐标,利用待定系数法,即可求得直线的解析式.
(2)根据比例的性质求得BD的长,即可求得D的坐标,利用待定系数法,即可求得直线的解析式.
解答: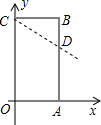 解:(1)B点坐标为(3,5).
解:(1)B点坐标为(3,5).
(2)∵过点C的直线CD交AB边于点D,且把矩形OABC的周长分为1:3两部分,
OC=AB>BD,OA=BC,
则一定有:
=
,
即
=
,
解得BD=1,
∴AD=AB-BD=5-1=4,
即D点的坐标为(3,4),
设直线CD的关系式为y=kx+b,且经过(0,5)和(3,4)得,
,
解之得
,
即直线CD的关系式为:y=-
x+5.
 解:(1)B点坐标为(3,5).
解:(1)B点坐标为(3,5).(2)∵过点C的直线CD交AB边于点D,且把矩形OABC的周长分为1:3两部分,
OC=AB>BD,OA=BC,
则一定有:
| CB+BD |
| CO+OA+AB-BD |
| 1 |
| 3 |
即
| 3+BD |
| 13-BD |
| 1 |
| 3 |
解得BD=1,
∴AD=AB-BD=5-1=4,
即D点的坐标为(3,4),
设直线CD的关系式为y=kx+b,且经过(0,5)和(3,4)得,
|
解之得
|
即直线CD的关系式为:y=-
| 1 |
| 3 |
点评:本题主要考查了矩形的性质,比例的性质,以及待定系数法求函数解析式.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).
如图矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(3,0)、(0,5).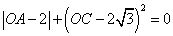 .
.