题目内容
如图,矩形OABC在平面直角坐标系中,若OA、OC的长满足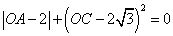
.
⑴求B、C两点的坐标.
⑵把△ABC沿AC对折,点B落在点B′处,线段AB′与x轴交于点D,求直线BB′的解析式．
⑶在直线BB′上是否存在点P,使△ADP为直角三角形？若存在,请直接写出
P 点坐标；若不存在,请说明理由.
【答案】
(1) 依题意，OA＝2，OC＝2
∵ 四边形OABC是矩形
∴ BC＝OA＝2
故B（2，2），C（2，0）
(2) 计算出B′（，－1）
设直线BB′的解析式为y＝kx＋b，过B（2，2）和有B′（，－1）
2＝2k＋b －1＝k＋b 解得，k＝ b＝－4
∴y＝x－4
（3）存在，P1（3,5）；P2（，1）
【解析】略
练习册系列答案
相关题目
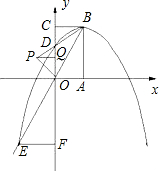如图矩形OABC，AB=2OA=2n，分别以OA和OC为x、y轴建立平面直角坐标系，连接OB，沿OB折叠，使点A落在P处．过P作PQ⊥y轴于Q．
.
