题目内容
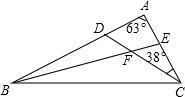 如图所示,D是AB上一点,E是AC上一点,BE、CD相交于F,∠A=63°,∠ACD=38°,∠ABE=20°.
如图所示,D是AB上一点,E是AC上一点,BE、CD相交于F,∠A=63°,∠ACD=38°,∠ABE=20°.(1)求∠BDC的度数;
(2)求∠BFC的度数;
(3)比较∠A、∠BDC和∠BFC的大小,并说明理由.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)直接运用三角形外角的性质即可解决问题.
(2)两次运用三角形外角的性质即可解决问题.
(3)根据(1)、(2)中的计算结果,经比较即可解决问题.
(2)两次运用三角形外角的性质即可解决问题.
(3)根据(1)、(2)中的计算结果,经比较即可解决问题.
解答: 解:(1)如图,∠BDC=∠A+∠ACD
解:(1)如图,∠BDC=∠A+∠ACD
=63°+38°=101°.
(2)∵∠BEC=∠A+∠ABE
=63°+20°=83°,
∴∠BFC=∠BEC+∠ACD
=83°+38°=121°.
(3)∵∠A=63°,∠BDC=101°,∠BFC=121°,
∴∠A<∠BDC<∠BFC.
 解:(1)如图,∠BDC=∠A+∠ACD
解:(1)如图,∠BDC=∠A+∠ACD=63°+38°=101°.
(2)∵∠BEC=∠A+∠ABE
=63°+20°=83°,
∴∠BFC=∠BEC+∠ACD
=83°+38°=121°.
(3)∵∠A=63°,∠BDC=101°,∠BFC=121°,
∴∠A<∠BDC<∠BFC.
点评:该题主要考查了三角形的内角和定理、外角的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
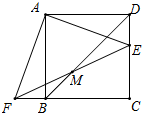 如图,正方形ABCD中,将∠BAD绕点A顺时针旋转,角的两边分别交CD边于点E,CB边的延长线点F上,连接EF交BD于点M.
如图,正方形ABCD中,将∠BAD绕点A顺时针旋转,角的两边分别交CD边于点E,CB边的延长线点F上,连接EF交BD于点M. “宝塔”是黄州城的古迹之一,有人想在塔外测量它的底角∠ABC的度数,如图,请问该如何测量?
“宝塔”是黄州城的古迹之一,有人想在塔外测量它的底角∠ABC的度数,如图,请问该如何测量? 如图:四边形ABCD内接于☉O,点P在BC的延长线上,且PD∥AC.求证:PC•AB=AD•CD.
如图:四边形ABCD内接于☉O,点P在BC的延长线上,且PD∥AC.求证:PC•AB=AD•CD.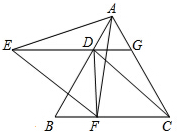 如图,△ABC是等边三角形,EG∥BC,DE=DB.EF∥DC,连接DF.
如图,△ABC是等边三角形,EG∥BC,DE=DB.EF∥DC,连接DF.