题目内容
13.下列各式成立的是( )| A. | $\frac{2}{a}$+$\frac{2}{b}$=$\frac{4}{a+b}$ | B. | $\frac{3}{k+3}$=$\frac{1}{k}$ | ||
| C. | ($\frac{m}{{n}^{2}}$)2=$\frac{{m}^{2}}{{n}^{2}}$ | D. | $\frac{0.2x+y}{3x-0.4y}$=$\frac{x+5y}{15x-2y}$ |
分析 根据分式的加减法则、分式乘方的法则对各选项进行逐一分析即可.
解答 解:A、左边=$\frac{2(b+a)}{ab}$≠右边,故本选项错误;
B、左边是最简分式,不能再进行化简,故本选项错误;
C、左边=$\frac{{m}^{2}}{{n}^{4}}$≠右边,故本选项错误;
D、左边=$\frac{5(0.2x+y)}{5(3x-0.4y)}$=$\frac{x+5y}{15x-2y}$=右边,故本选项正确.
故选D.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
3. 如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
 如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )
如图,点A和点D都在线段BC的垂直平分线上.连接AB,AC,DB,DC.如果∠1=20°,∠2=50°.那么∠BAC比∠BDC( )| A. | 大40° | B. | 小40° | C. | 大30° | D. | 小30° |
1. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 肇 | D. | 庆 |
3. 如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )
如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )
 如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )
如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥x轴,交双曲线y=-$\frac{3}{x}$(x<0)于点B,若OA⊥OB,则$\frac{OA}{OB}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{6}}{2}$ |
 如图,直线AB,CD相交于点O,OE平分∠BOD,若∠AOE=144°,则∠AOC的度数是72°.
如图,直线AB,CD相交于点O,OE平分∠BOD,若∠AOE=144°,则∠AOC的度数是72°. 如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE.
如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE.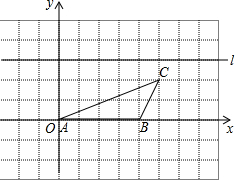 如图,在平面直角坐标系中,△ABC的边AB与x轴重合,点C的坐标是(5,2),在△ABC的上方有一直线l与x轴平行;
如图,在平面直角坐标系中,△ABC的边AB与x轴重合,点C的坐标是(5,2),在△ABC的上方有一直线l与x轴平行;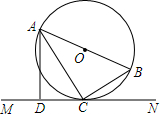 如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.求证:MN是⊙O的切线.
如图,AB是⊙O的直径,C是⊙O上一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC.求证:MN是⊙O的切线.