题目内容
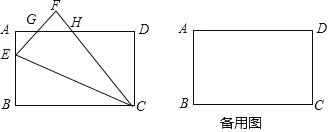
【题目】如图所示,四边形![]() 为正方形,
为正方形,![]() 为
为![]() 上一点,将正方形折叠,使点
上一点,将正方形折叠,使点![]() 与点
与点![]() 重合,折痕为
重合,折痕为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() .求:
.求:
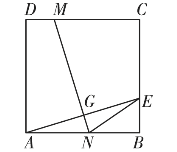
(1)![]() 的面积;
的面积;
(2)![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先由tan∠AEN=![]() ,DC+CE=10可得出BE=
,DC+CE=10可得出BE=![]() AB,再由翻折变换的性质得出∠AEN=∠EAN,所以可以先设BE=a,从而求出AB=3a,CE=2a进而求出a的值, 由a的值可得出AB=6,CE=4.求出底AD的长,然后再由tan∠AEN与边的关系,求出高,最后利用面积公式求面积;
AB,再由翻折变换的性质得出∠AEN=∠EAN,所以可以先设BE=a,从而求出AB=3a,CE=2a进而求出a的值, 由a的值可得出AB=6,CE=4.求出底AD的长,然后再由tan∠AEN与边的关系,求出高,最后利用面积公式求面积;
(2)sin∠ENB的值用正弦定义求即可.
解:(1)由折叠可知:MN为AE的垂直平分线,
∴AN=EN,
∴∠EAN=∠AEN(等边对等角),
∴tan∠AEN=tan∠EAN=![]() ,
,
∴设BE=a,AB=3a,则CE=2a,
∵DC+CE=10,
∴3a+2a=10,
∴a=2,
设MN与AE交于点G,
∵由(1)知a=2,
∴AB=6,CE=4,
∵AE=![]() ,
,
∴EG=![]() AE=
AE=![]() ×2
×2![]() =
=![]() ,
,
又∵![]() ,
,
∴NG=![]() ,
,
∴AN=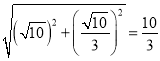 ,
,
∴AN=NE=![]() ,
,
∴S△ANE=![]() ;
;
(2)∵Rt△ENB中,EB=2,NE=![]() ,
,
∴sin∠ENB=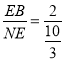 =
=![]() .
.

练习册系列答案
相关题目