题目内容
满足不等式2n-5<5-2n的所有正整数的和为 .
考点:一元一次不等式的整数解
专题:
分析:先解得不等式2n-5<5-2n的解集为n<2.5,则不等式2n-5<5-2n的正整数解为1,2,然后把它们相加即可.
解答:解:移项、合并同类项得4n<10,
系数化为1得n<2.5,
所以不等式2n-5<5-2n的正整数解为1,2,
所以所有正整数解之和=1+2=3.
故答案为3.
系数化为1得n<2.5,
所以不等式2n-5<5-2n的正整数解为1,2,
所以所有正整数解之和=1+2=3.
故答案为3.
点评:本题考查了一元一次不等式的整数解:先求出一元一次不等式的解集,然后在解集里找出整数,这些整数就是一元一次不等式的整数解.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
下列函数中,图象经过原点的函数是( )
| A、y=x-5 | ||
| B、y=-x+1 | ||
C、y=
| ||
| D、y=-2x |
 如图,已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.
如图,已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.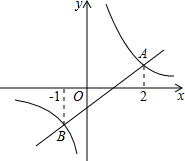 如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=
如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=