题目内容
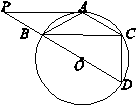
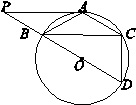
已知如图:△ABC内接于⊙O,P为BC边延长线上的一点,PA为⊙O的切线,切点为A,若PA=6,PC=4,求 的值.
的值.
【答案】分析:由于∠B、∠ABC都不在直角三角形中,因此需要通过作辅助线来达到这个目的.过A作⊙O的直径AD,连接BD、CD,那么∠ADB=∠ACB、∠ADC=∠B,在Rt△ABD和Rt△ACD中,可得到sinB=AC:AD,sinACB=AB:AD;因此只需求得AB:AC的值即可,分析图形,可通过证△PAB∽△PCA来求得这个比值.
解答: 解:∵PA是⊙O的切线,
解:∵PA是⊙O的切线,
∴PA2=PC•PB,
∵PA=6,PC=4,
∴PB=9;
由弦切角定理知:∠PAC=∠ABC,
又∵∠APC=∠BPA,
∴△PAC∽△PBA,
∴ ;
;
过A作⊙O的直径AD,连接BD、CD;
则有:∠ADB=∠ACB,∠ABC=∠ADC;
在Rt△ABD中,sinADB=sinACB=AB:AD,
同理得:sinADC=sinABC=AC:AD;
∴ =
= .
.
点评:此题主要考查了圆周角定理、切线的性质、弦切角和切割线定理以及相似三角形的判定和性质;能够通过作辅助线将所求的角转移到相应的直角三角形中,是解答此题的关键.
解答:
 解:∵PA是⊙O的切线,
解:∵PA是⊙O的切线,∴PA2=PC•PB,
∵PA=6,PC=4,
∴PB=9;
由弦切角定理知:∠PAC=∠ABC,
又∵∠APC=∠BPA,
∴△PAC∽△PBA,
∴
 ;
;过A作⊙O的直径AD,连接BD、CD;
则有:∠ADB=∠ACB,∠ABC=∠ADC;
在Rt△ABD中,sinADB=sinACB=AB:AD,
同理得:sinADC=sinABC=AC:AD;
∴
 =
= .
.点评:此题主要考查了圆周角定理、切线的性质、弦切角和切割线定理以及相似三角形的判定和性质;能够通过作辅助线将所求的角转移到相应的直角三角形中,是解答此题的关键.

练习册系列答案
相关题目
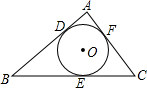 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
 已知如图:△ABC内接于⊙O,P为BC边延长线上的一点,PA为⊙O的切线,切点为A,若PA=6,PC=4,求
已知如图:△ABC内接于⊙O,P为BC边延长线上的一点,PA为⊙O的切线,切点为A,若PA=6,PC=4,求