Question

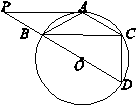
已知:如图，△ABC内接于⊙O，且AB=AC=13，BC=24，PA∥BC，割线PBD过圆心，交⊙O于另一个点D，联结CD．

1.⑴求证：PA是⊙O的切线；

2.⑵求⊙O的半径及CD的长．

 

Answer 1

 

1.证明：（1）联结OA、OC，设OA交BC于G．

∵AB=AC，

∴

∴AOB=AOC.

∵OB=OC，

∴OA⊥BC．

∴OGB=90°

 ∵PA∥BC，

∴OAP=OGB=90°

∴OA⊥PA． 

∴PA是⊙O的切线．

2.（2）∵AB=AC，OA⊥BC，BC=24 

∴BG=BC=12．

   ∵AB=13，  

 ∴AG=．                         …………………3分

设⊙O的半径为R，则OG=R－5．

在Rt△OBG中，∵，

． 

 解得，R=16.9                                   …………………4分

∴OG=11.9．

∵BD是⊙O的直径，

∴O是BD中点， 

  ∴OG是△BCD的中位线．

∴DC=2OG=23.8．

解析:略