题目内容
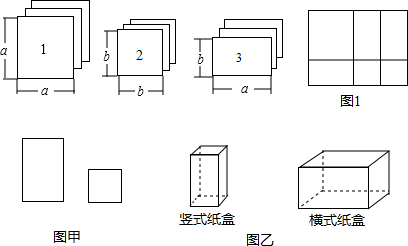
2.有足够多的长方形和正方形卡片,如图:(1)如果选取1号、2号、3号卡片分别为1张、2张、3张,可拼成一个图(1)长方形(不重叠无缝隙),这个长方形的面积既可以表示为(a+2b)(a+b),又可表示为a2+3ab+2b2,所以根据面积相等可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(2)如果选取1号、2号、3号卡片分别为2张、2张、5张,可拼成一个长方形(不重叠无缝隙),请画出这个长方形的草图,并运用拼图前后面积之间的关系得出一个等式.
(3)小明要拼一个长为5a+9b,宽为3a+7b的长方形,那么需用1号卡片15张,2号卡片63张,3号卡片62张.
分析 (1)根据面积相等可得等式:(a+2b)(a+b)=a2+3ab+2b2;
(2)画出相关草图,表示出拼合前后的面积即可;
(3)得到所给矩形的面积,看有几个a2,几个b2,几个ab即可.
解答 解:(1)(a+2b)(a+b)=a2+3ab+2b2;
(2)如图所示:
故答案为:2a2+5ab+2b2=(2a+b)(a+2b);
(2)(5a+9b)(3a+7b)=15a2+35ab+27ab+63b2=15a2+62ab+63b2,
需用1号卡片15张,2号卡片63张,3号卡片62张.
故答案为:a2+3ab+2b2;15,63,62.
点评 本题主要考查了多项式乘多项式,用到的知识点是长方形的面积公式和正方形的面积公式以及多项式乘多项式的法则.

练习册系列答案
相关题目
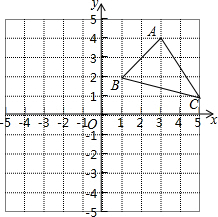 如图,在所给网格图(每小格边长均为1的正方形)中完成下列各题:
如图,在所给网格图(每小格边长均为1的正方形)中完成下列各题: