题目内容
11.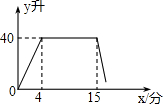 妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:(1)洗衣机的进水时间是4分钟;
(2)清洗时洗衣机中的水量是40 升;
(3)洗衣机的清洗时间为11分钟;
(4)已知洗衣机的排水速度为每分钟19升,如果排水时间为2分钟,则排水结束时洗衣机中剩下的水量为2升.
分析 由图象可知0-4分时是进水时间,4-15分钟时时清洗时间,15分钟以后是放水的时间,由此即可一一求解.
解答 解:(1)由图可知洗衣机的进水时间是4分钟.
(2)清洗时洗衣机中的水量是40升.
(3)洗衣机的清洗时间=15-4=11分钟.
(4)∵排水的时间是2分钟,排水速度为每分钟19升
∴排水结束时洗衣机中剩下的水量是40-2×19=2(升).
故答案分别为4,40,11,2.
点评 本题主要一次函数的应用,解题的关键是读懂图象信息,利用图中信息解决问题,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
7.某班级第3组第4排位置可以用数对(3,4)表示,则数对(1,2)表示的位置是( )
| A. | 第2组第1排 | B. | 第1组第1排 | C. | 第1组第2排 | D. | 第2组第2排 |
6.已知二次函数y=-2(x-m)2+n满足m+n=-7,mn=7,则下列关于函数值y的说法正确的是( )
| A. | y恒大于0 | B. | y恒小于0 | C. | y是非正数 | D. | 无法确定 |
16.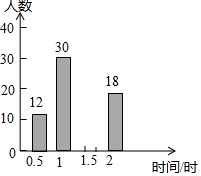 在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:
在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:
(1)统计表中的m=100,x=40,y=0.18.
(2)被调查同学劳动时间的中位数是1.5;
(3)请将频数分布直方图补充完整.
 在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:
在西安市开展“美丽城市,创卫同行”活动中,我校倡议七年级学生利用双休日在各自社区参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制不完整的统计图表,如图所示:| 劳动时间(时)0.5 | 频数(人数)12 | 频率0.12 |
| 1 | 30 | 0.3 |
| 1.5 | x | 0.4 |
| 2 | 18 | y |
| 合计 | m | 1 |
(2)被调查同学劳动时间的中位数是1.5;
(3)请将频数分布直方图补充完整.
3.若反比例函数y=$\frac{k+1}{x}$的图象经过点(2,3),则k的值为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
20.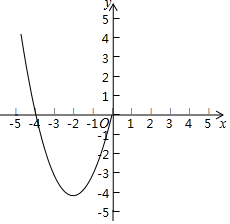 某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
(1)补全上表;
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当x取何值时,y随x的增大而增大?
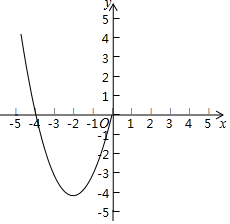 某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
某数学兴趣小组对函数y=x2-4|x|的图象和性质进行探究,发现自变量x的取值范围是全体实数,x与y的几组对应值列表如下:| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | -3 | -4 | -3 | 0 | -3 | … |
(2)根据表中数据,画出函数图象的另一部分;
(3)进一步探究函数图象,回答问题:
①观察图象可以得出,对应的方程x2-4|x|=0有3个实数根;
②关于x的方程x2-4|x|=a有2个实数根时,a的取值范围是a=-4或a>0;
③当x取何值时,y随x的增大而增大?
 如图,在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(x>0)的图象与直线y=x-2交于点A(3,m).
如图,在平面直角坐标系xOy中,函数y=$\frac{k}{x}$(x>0)的图象与直线y=x-2交于点A(3,m).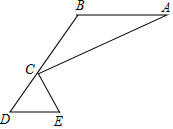 如图,AB∥DE,C为BD上一点,∠A=∠BCA,∠E=∠ECD,求证:CE⊥CA.
如图,AB∥DE,C为BD上一点,∠A=∠BCA,∠E=∠ECD,求证:CE⊥CA.