题目内容
5. 如图,流经某市的一条河流的两岸互相平行,河岸l1上有一排观赏灯,已知相邻两灯之间的距离AB=10米,某人在河岸l2的C处测得∠ACE=60°,然后沿河岸向右走了90米到达D处,测得∠BDC=30°.求河流的宽度.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,流经某市的一条河流的两岸互相平行,河岸l1上有一排观赏灯,已知相邻两灯之间的距离AB=10米,某人在河岸l2的C处测得∠ACE=60°,然后沿河岸向右走了90米到达D处,测得∠BDC=30°.求河流的宽度.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 过点A作AF∥BD交l2于点F.利用l1∥l2,AF∥DB,得到四边形AFDB是平行四边形,利用平行四边形的性质得到DF=AB=10,∠AFC=30°从而得到CF=CD-DF=90-10=80,然后利用∠ACE是△ACF的一个外角,得∠CAF=∠ACE-∠AFC=60°-30°=30°,得到进而AC=CF=80.然后在Rt△AEC中求得AE的长即可.
解答 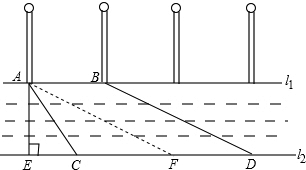 解:过点A作AF∥BD交l2于点F.
解:过点A作AF∥BD交l2于点F.
∵l1∥l2,AF∥DB,
∴四边形AFDB是平行四边形.
∴DF=AB=10,∠AFC=30°,
∴CF=CD-DF=90-10=80.
又∵∠ACE是△ACF的一个外角,
∴∠CAF=∠ACE-∠AFC=60°-30°=30°,
∴∠CAF=∠AFC.
∴AC=CF=80.
在Rt△AEC中,∠ACE=60°
∴AE=AC•sin60°=80×$\frac{\sqrt{3}}{2}$≈69.28≈69.3(米).
答:河流的宽度AE约为69.3米.
点评 本题考查了解直角三角形的应用,规则图形可以通过作平行线转化为平行四边形与直角三角形的问题进行解决.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
15.在精准扶贫中,某村的李师傅在县政府的扶持下,去年下半年,他对家里的3个温室大棚进行修整改造,然后,1个大棚种植香瓜,另外2个大棚种植甜瓜,今年上半年喜获丰收,现在他家的甜瓜和香瓜已全部售完,他高兴地说:“我的日子终于好了”.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
现假设李师傅今年下半年香瓜种植的大棚数为x个,明年上半年8个大棚中所产的瓜全部售完后,获得的利润为y元.
根据以上提供的信息,请你解答下列问题:
(1)求出y与x之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
最近,李师傅在扶贫工作者的指导下,计划在农业合作社承包5个大棚,以后就用8个大棚继续种植香瓜和甜瓜,他根据种植经验及今年上半年的市场情况,打算下半年种植时,两个品种同时种,一个大棚只种一个品种的瓜,并预测明年两种瓜的产量、销售价格及成本如下:
| 品种 项目 | 产量(斤/每棚) | 销售价(元/每斤) | 成本(元/每棚) |
| 香瓜 | 2000 | 12 | 8000 |
| 甜瓜 | 4500 | 3 | 5000 |
根据以上提供的信息,请你解答下列问题:
(1)求出y与x之间的函数关系式;
(2)求出李师傅种植的8个大棚中,香瓜至少种植几个大棚?才能使获得的利润不低于10万元.
16.下列标志图中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是$\frac{1}{3}$,那么另一组数据3x1+1,3x2+1,3x3+1,3x4+1,3x5+1的平均数和方差分别是( )
| A. | 2,$\frac{1}{3}$ | B. | 2,1 | C. | 7,3 | D. | 3,3 |
17. 如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
 如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
如图,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )| A. | ∠ECD=112.5° | B. | DE平分∠FDC | C. | ∠DEC=30° | D. | AB=$\sqrt{2}$CD |
12.为了了解某区八年级学生的体重情况,从中抽取了200名学生进行体重测试.在这个问欢迎登陆全品中考网“题中,下列说法错误的是( )
| A. | 200名学生的体重是一个样本 | B. | 200名是样本容量 | ||
| C. | 每个学生的体重是个体 | D. | 全县八年级学生的体重是总体 |