题目内容
14. 如图,在⊙O1中,AB为直径,AB=4,点C在⊙O1上,连接AC,以AC为直径作⊙O2,⊙O1在⊙O2的内部,⊙O2的面积为3π,点D在AB上运动,当线段CD的长度最短时,AD的长度为( )
如图,在⊙O1中,AB为直径,AB=4,点C在⊙O1上,连接AC,以AC为直径作⊙O2,⊙O1在⊙O2的内部,⊙O2的面积为3π,点D在AB上运动,当线段CD的长度最短时,AD的长度为( )| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
分析 当CD⊥AB时,线段CD的长度最短,由AC是⊙O2的直径,得到点D是AB与⊙O2的交点,如图,连接BC,根据⊙O2的面积为3π,得到AC=2$\sqrt{3}$,解直角三角形即可得到结论.
解答  解:当CD⊥AB时,线段CD的长度最短,
解:当CD⊥AB时,线段CD的长度最短,
∵AC是⊙O2的直径,
∴点D是AB与⊙O2的交点,如图,
连接BC,
∵⊙O2的面积为3π,
∴AC=2$\sqrt{3}$,
∴cos∠A=$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$,
∴∠A=60°,
∴AD=3.
点评 本题考查了圆周角定理,解直角三角形,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )
如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )
 如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )
如图所示的图形是按下列步骤做得的:①在直线l上截取线段AB,使AB=2;②分别以A,B为圆心,以1.5为半径作弧,两弧分别交于C,D两点,连接AC,AD,BC,BD,则四边形ACBD的面积是( )| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
19.下列各数中,最大的数是( )
| A. | -2 | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
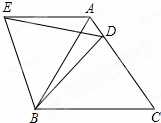 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED.
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED. 如图是两个重叠的直角三角形,将其中一个直角三角形沿着BC方向平移BE的长度就得到该图形,求阴影部分的面积(单位:厘米)
如图是两个重叠的直角三角形,将其中一个直角三角形沿着BC方向平移BE的长度就得到该图形,求阴影部分的面积(单位:厘米)
 如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P.则tan∠APD的值是( )
如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P.则tan∠APD的值是( )