题目内容
1.m是方程2x2+3x-1=0的根,则式子4m2+6m+2014的值为2016.分析 根据一元二次方程的解的定义,将x=m代入已知方程后即可求得所求代数式的值.
解答 解:把x=m代入2x2+3x-1=0,得
2m2+3m-1=0,
则2m2+3m=1.
所以4m2+6m+2014=2(2m2+3m)+2014=2+2014=2016.
故答案为:2016.
点评 本题考查了一元二次方程的解的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.

练习册系列答案
相关题目
11.小明所在班级有16名男生报名参加校运动会,他们的身高(单位:cm)如下:
170 165 178 166 173 163 178 172
170 174 170 170 174 178 178 178
(1)将这16名男生的身高由矮到高排列,统计每种身高的频数和频率,并填如表.
(2)身高超过170cm的同学有几名?约占总人数的百分之几?(精确到1%)
170 165 178 166 173 163 178 172
170 174 170 170 174 178 178 178
(1)将这16名男生的身高由矮到高排列,统计每种身高的频数和频率,并填如表.
| 身高/cm | ||||||||
| 频数 | ||||||||
| 频率 |
6.1.252012×($\frac{4}{5}$)2014的值是( )
| A. | $\frac{4}{5}$ | B. | $\frac{16}{25}$ | C. | 1 | D. | -1 |
13.化简a2•a3的结果是( )
| A. | a-1 | B. | a | C. | a5 | D. | a6 |
10. 如图,点A,B,C在同一条直线上,则图中的线段共有( )
如图,点A,B,C在同一条直线上,则图中的线段共有( )
 如图,点A,B,C在同一条直线上,则图中的线段共有( )
如图,点A,B,C在同一条直线上,则图中的线段共有( )| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
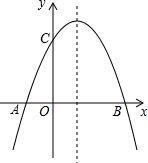 抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点.
抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点. 有理数a、b、c在数轴上的位置如图所示,试化简:
有理数a、b、c在数轴上的位置如图所示,试化简: 如图,△ABC的三条角平分线交于O点,已知△ABC的周长为20,OD⊥AB,OD=5,则△ABC的面积=50.
如图,△ABC的三条角平分线交于O点,已知△ABC的周长为20,OD⊥AB,OD=5,则△ABC的面积=50.