题目内容
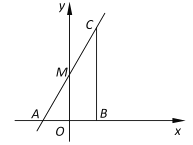
【题目】如图，已知点
、
在直线
上，点
在线段
上，
与
交于点
，
．求证：
.（完成以下填空）
证明：∵
（已知），
且
（ ）
∴
（等量代换）
∴ 
（ ）
∴
（ ）
又∵
（已知）
∴
（等量代换）
∴（ ）
【答案】对顶角相等；CE；GF；同位角相等，两直线平行；两直线平行，同位角相等；内错角相等，两直线平行．
【解析】
根据同位角相等两直线平行，可证CE∥GF，进而利用平行线的性质和判定证明．
证明：∵
（已知），
且
（对顶角相等 ）
∴
（等量代换）
∴ CE 
GF （ 同位角相等，两直线平行 ）
∴
（ 两直线平行，同位角相等 ）
又∵
（已知）
∴
（等量代换）
∴
（ 内错角相等，两直线平行 ）
故答案为对顶角相等；CE；GF；同位角相等，两直线平行；两直线平行，同位角相等；内错角相等，两直线平行．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
