Question

【题目】已知：如图，在直角坐标平面中，点在轴的负半轴上，直线经过点，与轴相交于点，点是点关于原点的对称点，过点的直线轴，交直线于点，如果．

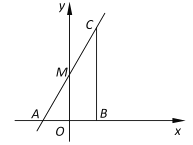
（1）求直线的表达式；

（2）如果点在直线上，且是等腰三角形，请求出点的坐标．

Answer 1

【答案】（1）；（2）或．

【解析】

（1）先求出点M的坐标，从而可得OM的长，再根据直角三角形的性质可得OA的长，从而可得点A的坐标，然后利用待定系数法求解即可；

（2）先根据对称性得出点B的坐标，再根据两点之间的距离公式可得的长，然后根据等腰三角形的定义分三种情况建立等式求解即可．

（1）对于

当时，，则点的坐标为

设

∵

在中，，

则有

解得，即

∴点的坐标为

∵直线经过点

∴，解得

故直线的表达式为；

（2）点是点关于原点的对称点

点的坐标为

设直线上的点坐标为

则

由等腰三角形的定义，分以下三种情况：

①当时，是等腰三角形

则，解得或

或

此时，点D的坐标为或

②当时，是等腰三角形

则，解得或

或

此时，点D的坐标为或（与点重合，不能构成三角形，舍去）

③当时，是等腰三角形

则，解得

此时，点的坐标为

综上，点的坐标为点或．