题目内容
已知x2+y2+xy-3y+3=0,求xy的值.
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:把x2+y2+xy-3y+3=0变形为两个完全平方的和为0的形式,再根据非负数的性质求出x,y的值,最后代入计算即可.
解答:解:由x2+y2+xy-3y+3=0,得
x2+xy+
y2+
y2-3y+3=0,
∴(x+
y)2+3(
y-1)2=0,
∴x+
y=0,
y-1=0,
∴y=2,x=-1,
∴xy=(-1)2=1.
x2+xy+
| 1 |
| 4 |
| 3 |
| 4 |
∴(x+
| 1 |
| 2 |
| 1 |
| 2 |
∴x+
| 1 |
| 2 |
| 1 |
| 2 |
∴y=2,x=-1,
∴xy=(-1)2=1.
点评:此题考查了非负数的性质,用到的知识点是完全平方公式,关键是把x2+y2+xy-3y+3=0变形为(x+
y)2+3(
y-1)2=0.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
若把分式
中的x和y都扩大3倍,那么分式的值( )
| x+y |
| 2xy2 |
| A、扩大3倍 | ||
| B、不变 | ||
| C、缩小3倍 | ||
D、缩小为
|
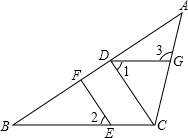 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.
如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整. 如图所示,在平面直角坐标系中,直线y=0.5x-1与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是( )
如图所示,在平面直角坐标系中,直线y=0.5x-1与矩形ABCO的边OC、BC分别交于点E、F,已知OA=3,OC=4,则△CEF的面积是( )