题目内容
阅读下列例题:
解方程:|2x|=1.
解:①当2x≥0时,原方程可化为2x=1,所以x=
;
②当2x<0时,原方程可化为-2x=1,所以x=-
.
所以原方程的解是x=
或x=-
.
依照例题解方程:|3x+1|=5.
解方程:|2x|=1.
解:①当2x≥0时,原方程可化为2x=1,所以x=
| 1 |
| 2 |
②当2x<0时,原方程可化为-2x=1,所以x=-
| 1 |
| 2 |
所以原方程的解是x=
| 1 |
| 2 |
| 1 |
| 2 |
依照例题解方程:|3x+1|=5.
考点:含绝对值符号的一元一次方程
专题:阅读型
分析:根据分类讨论:x≥-
,x<-
,可化简绝对值,解方程,可得答案.
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:①当x≥-
时,原方程可化为3x+1=5,解得x=
;
②当x<-
时,原方程可化为-3x-1=5,解得x=-2;
综上所述:原方程的解是x=
,x=-2.
| 1 |
| 3 |
| 4 |
| 3 |
②当x<-
| 1 |
| 3 |
综上所述:原方程的解是x=
| 4 |
| 3 |
点评:本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图:已知AB,CD相交于点O,且AB=DC,AC=DB,求证:∠A=∠D.
如图:已知AB,CD相交于点O,且AB=DC,AC=DB,求证:∠A=∠D. 如图,直线y=x+4与x轴、y轴分别交于A、B两点,直线y=-x+b过点B且与x轴交于点C.求直线BC的表达式.
如图,直线y=x+4与x轴、y轴分别交于A、B两点,直线y=-x+b过点B且与x轴交于点C.求直线BC的表达式. 如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.
如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竿长1米时它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m,这样∠α就可以计算出来了,请你算一算.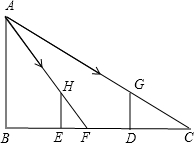 如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.
如图,小明站在竖立的电线杆AB前D处时,经过头顶的光线与地面所成的角为∠ACB,tan∠ACB=0.6.他朝电线杆走了4m到达E处时,经过头顶的光线与地面所成的角为∠AFB,tan∠AFB=1.8,已知小明的身高为1.8m,求电线杆的长.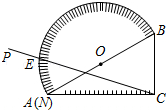 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第27秒,点E在量角器上对应的读数是
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第27秒,点E在量角器上对应的读数是