题目内容

(
1
2
a-b)(-
1
2
a-b)=（　　）
分析：利用平方差公式进行计算即可得解．
解答：解：（
1
2
a-b）（-
1
2
a-b）=-
1
4
a2+b2．
故选B．
点评：本题考查了平方差公式，运用平方差公式计算时，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方．
练习册系列答案
相关题目
（1）先化简，再求值：
1
4
(-4a2+2a-8)-(
1
2
a-2)，其中a=
1
2
；
（2）已知a+b=5，a-c=4，求代数式（b+c）2+2（b+c）-1的值．
精英家教网如图，P为△ABC的边BC上的任意一点，设BC=a，
当B1、C1分别为AB、AC的中点时，B1C1=
1
2
a，
当B2、C2分别为BB1、CC1的中点时，B2C2=
3
4
a，
当B3、C3分别为BB2、CC2的中点时，B3C3=
7
8
a，
当B4、C4分别为BB3、CC3的中点时，B4C4=
15
16
a，
当B5、C5分别为BB4、CC4的中点时，B5C5=
 
，
…
当Bn、Cn分别为BBn-1、CCn-1的中点时，则BnCn=
 
；
设△ABC中BC边上的高为h，则△PBnCn的面积为
 
（用含a、h的式子表示）．
最简根式
4a-24a+3b
和
b+12a-b+6
是同类根式，则a=
1
1
，b=
1
1
．
（1998•南京）下列计算中，正确的是（　　）
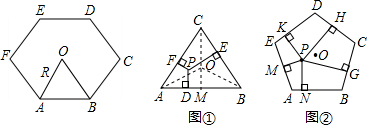（2012•青岛模拟）同学们已经认识了很多正多边形，现以正六边形为例再介绍与正多边形相关的几个概念．如正六边形ABCDEF各边对称轴的交点O，又称正六边形的中心，其中OA称正六边形的半径，通常用R表示，∠AOB称为中心角，显然．提出问题：正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
探索发现：
（1）为了解决这个问题，我们不妨从最简单的正多边形--正三角形入手．
如图①，△ABC是正三角形，半径OA=R，∠AOB是中心角，P是△ABC内任意一点，P到△ABC各边距离分别为h1、h2、h3 ，确定h1+h2+h3的值与△ABC的半径R及中心角的关系．
解：设△ABC的边长是a，面积为S，显然S=
1
2
a（h1+h2+h3）
O为△ABC的中心，连接OA、OB、OC，它们将△ABC分成三个全等的等腰三角形，过点O作OM⊥AB，垂足为M，Rt△AOM中，易知
OM=OAcos∠AOM=Rcos
1
2
∠AOB=Rcos
1
2
×120°=Rcos60°，
AM=OAsin∠AOM=Rsin
1
2
∠AOB=Rsin
1
2
×120°=Rcos60°
∴AB=a=2AM=2Rsin60°
∴S△AOB=
1
2
AB×OM=
1
2
×2Rsin60°•Rcos60°=R2sin60°cos60°
∴S△ABC=3S△AOB=3R2sin60°cos60°
∴
1
2
a（h1+h2+h3）=3R2sin60°cos60°
即：
1
2
×2Rsin60°（h1+h2+h3）=3R2sin60°cos60°
∴h1+h2+h3=3Rcos60°
（2）如图②，五边形ABCDE是正五边形，半径是R，P是正五边形ABCDE内任意一点，P到五边形ABCDE各边距离分别为h1、h2、h3、h4、h5，参照（1）的探索过程，确定h1+h2+h3+h4+h5的值与正五边形ABCDE的半径R及中心角的关系．
（3）类比上述探索过程，直接填写结论
正六边形（半径是R）内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6=
6Rcos30°
6Rcos30°

正八边形（半径是R）内任意一点P到各边距离之和 h1+h2+h3+h4+h5+h6+h7+h8=
8Rcos22.5°
8Rcos22.5°

正n边形（半径是R）内任意一点P到各边距离之和  h1+h2+…+hn=
nRcos
180°
n
nRcos
180°
n
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网