题目内容
17.把下列各数填入相应的集合内:7.5,$\sqrt{15}$,4,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,$\root{3}{-27}$,0.31,-π,0.$\stackrel{•}{1}$$\stackrel{•}{5}$
(1)有理数集合{7.5,4,$\frac{2}{3}$,$\root{3}{-27}$,0.31,0.$\stackrel{•}{1}$$\stackrel{•}{5}$,…}
(2)无理数集合{$\sqrt{15}$,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,-π,…}
(3)正实数集合{7.5,$\sqrt{15}$,4,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,0.31,0.$\stackrel{•}{1}$$\stackrel{•}{5}$…}
(4)负实数集合{$\root{3}{-27}$,-π…}.
分析 首先实数可以分为有理数和无理数,无限不循环小数称之为无理数,除了无限不循环小数以外的数统称有理数;正整数、0、负整数统称为整数;正实数是大于0的所有实数,负实数是小于0的所有实数,由此即可求解.
解答 解:(1)有理数集合{7.5,4,$\frac{2}{3}$,$\root{3}{-27}$,0.31,0.$\stackrel{•}{1}$$\stackrel{•}{5}$,…}
(2)无理数集合{$\sqrt{15}$,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,-π,…}
(3)正实数集合{7.5,$\sqrt{15}$,4,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,0.31,0.$\stackrel{•}{1}$$\stackrel{•}{5}$…}
(4)负实数集合{$\root{3}{-27}$,-π,…}
故答案为:7.5,4,$\frac{2}{3}$,$\root{3}{-27}$,0.31,0.$\stackrel{•}{1}$$\stackrel{•}{5}$;$\sqrt{15}$,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,-π;7.5,$\sqrt{15}$,4,$\sqrt{\frac{9}{17}}$,$\frac{2}{3}$,0.31,0.$\stackrel{•}{1}$$\stackrel{•}{5}$;$\root{3}{-27}$,-π.
点评 本题考查了实数的分类与意义,熟练掌握实数的分类是解决问题的关键.

练习册系列答案
相关题目
8.下列式子成立的是( )
| A. | xy2-2y2•x=-xy2 | B. | 3a+5b=8ab | C. | 3ab-ab=2 | D. | a3•a2=a6 |
2.在同一坐标系中,抛物线y=x2,y=-x2的共同性质是( )
| A. | 关于y轴对称,开口向上 | B. | 关于y轴对称,顶点坐标为(0,0) | ||
| C. | 关于x轴对称,开口向下 | D. | 关于x轴对称,都有最高点 |
7.已知函数y=-$\frac{5}{4}$x2,点A(-1,y1)、B(-2,y2)、C(-3,y3)均在该函数的图象上,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y1<y3<y2 | D. | y2<y1<y3 |
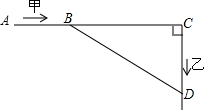 如图,东西方向上有A,C两地相距10km,甲以16km/h的速度从A地出发向正东方向前进,乙以12km/h的速度从C地出发向正南方向前进,问:最快经过多少小时,甲、乙两人相距6km?
如图,东西方向上有A,C两地相距10km,甲以16km/h的速度从A地出发向正东方向前进,乙以12km/h的速度从C地出发向正南方向前进,问:最快经过多少小时,甲、乙两人相距6km? 如图,在△ABC中,∠ACB=90°,点D、E分别为AC、AB的中点,延长BC到F使$CF=\frac{1}{2}BC$.
如图,在△ABC中,∠ACB=90°,点D、E分别为AC、AB的中点,延长BC到F使$CF=\frac{1}{2}BC$. 已知:如图,点D、E分别在线段AC、AB 上,AD•AC=AE•AB,且$\frac{AD}{AE}$=$\frac{1}{2}$,S△ADB=4,试求△AEC的面积.
已知:如图,点D、E分别在线段AC、AB 上,AD•AC=AE•AB,且$\frac{AD}{AE}$=$\frac{1}{2}$,S△ADB=4,试求△AEC的面积.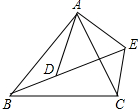 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$. 把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.
把-1,-2,-3,-4,-5,-6,-7,-8,-9填入图中方格中,使得每行的3个数,每列的3个数,斜对角的3个数相加都相等.