题目内容
20.已知点(2,y1),(3,y2)在反比例函数y=$\frac{-{k}^{2}-1}{x}$的图象上,则y1与y2的大小关系是( )| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 不确定 |
分析 先根据反比例函数的解析式判断出函数图象所在的象限,再根据各点横坐标的大小进行解答即可.
解答 解:∵-(k2+1)<0,
∴反比例函数的图象的两个分支分别位于二、四象限,且在每一象限内,y随x的增大而增大.
∵点(2,y1),(3,y2)都在第四象限.
∵2<3,
∴y1<y2.
故选:C.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
11.下列各图案中,是由一个基本图形通过平移得到的是( )
| A. |  | B. |  | C. |  | D. |  |
8.若|a|=2,|b|=5,则|a-b|的值等于( )
| A. | 3 | B. | 7 | C. | -7 | D. | 3或7 |
5.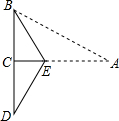 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
 如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )
如图所示,已知在三角形纸片ABC中,BC=4,AB=8,∠BCA=90°,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则DE的长度为( )| A. | 8 | B. | 4 | C. | $\frac{8}{3}$$\sqrt{3}$ | D. | $\frac{4}{3}$$\sqrt{3}$ |
9.计算(-3)-(-5)的结果等于( )
| A. | 8 | B. | -8 | C. | 2 | D. | -2 |