��Ŀ����
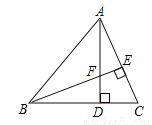
����ȫ�ȵ�ֱ��������ABC��DEF�ص���һ�����С�ACB=��DFE=90�㣬��A=��FDE=60�㣬AC=1. �̶���ABC����������DEF�������²�����
(1) ��ͼ (1)����DEF���߶�AB����ƽ��(��D�����߶�AB���ƶ�)������DC��CF��FB���ı���CDBF����״�ڲ��ϵı仯��������������仯������������.
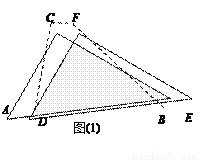
(2)��ͼ(2)����D���Ƶ�AB���е�ʱ����������ı���CDBF����״����˵������.

(3)��ͼ(3)����DEF��F��̶���AB���е㣬Ȼ����F�㰴˳ʱ�뷽����ת��DEF��ʹEF����AC������M��FD��BC��N����FM=x,FN=y,����y����x�ĺ�����ϵʽ��

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ


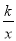 (x>0)��ͼ����ͼ����B��ͼ���ϣ�����OB���ӳ�����A��ʹAB��2OB������A��AC��y�ᣬ��y��
(x>0)��ͼ����ͼ����B��ͼ���ϣ�����OB���ӳ�����A��ʹAB��2OB������A��AC��y�ᣬ��y��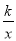 (x>0)��ͼ���ڵ�C������OC��S��AOC��5����k��__��
(x>0)��ͼ���ڵ�C������OC��S��AOC��5����k��__��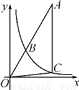
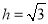 cm������뾶r=1cm����Բ��IJ����Ϊ_________cm2��
cm������뾶r=1cm����Բ��IJ����Ϊ_________cm2��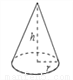
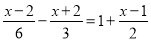 ��
�� ��x�ᡢy��ֱ���A��B���㣬��OΪ����ԭ�㣬���ڸ�����ƽ�������Ե�P�������A��B��O�غϣ�Ϊ�����ֱ����������Rt��ABOȫ�ȣ�������Ե�PΪ�����ֱ����������Rt��ABO��һ�������ߣ������з���������P�����Ϊ��������
��x�ᡢy��ֱ���A��B���㣬��OΪ����ԭ�㣬���ڸ�����ƽ�������Ե�P�������A��B��O�غϣ�Ϊ�����ֱ����������Rt��ABOȫ�ȣ�������Ե�PΪ�����ֱ����������Rt��ABO��һ�������ߣ������з���������P�����Ϊ��������