题目内容
4.在平面直角坐标系中,描出下列各点:A(-2,-1),B(4,-1),C(3,2),D(0,2),并计算四边形ABCD的面积.分析 先描点得到四边形ABCD为等腰梯形,然后根据梯形的面积公式计算即可.
解答 解:如图,
四边形ABCD的面积=$\frac{1}{2}$×(3+6)×3=$\frac{27}{2}$.
点评 本题考查了坐标与图形性质:利用点的坐标进行相应线段的长和判断线段与坐标轴的位置关系.解决本题的关键是画出几何图形得到四边形为等腰梯形.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.下列说法中,错误的是( )
| A. | 菱形的对角线互相平分 | B. | 正方形的对角线互相垂直平分 | ||
| C. | 矩形的对角线相等且平分 | D. | 等腰梯形的对角线相等且平分 |
14.不改变分式的值,下列各式中成立的是( )
| A. | $\frac{-a+5}{-a-5}=\frac{a+5}{a-5}$ | B. | $\frac{1}{-x+6}=\frac{-1}{x+6}$ | ||
| C. | $\frac{-x+y}{-x-y}=-\frac{x-y}{x+y}$ | D. | $\frac{-x}{y-3x}=\frac{x}{3x-y}$ |

 如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:AB=CD.
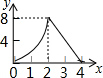
如图,在四边形ABCD中,∠B=∠D,∠1=∠2,求证:AB=CD. 如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )
如图,正方形ABCD的边长为4,动点M、N同时从A点出发,点M沿AB以每秒1个单位长度的速度向中点B运动,点N沿折现ADC以每秒2个单位长度的速度向终点C运动,设运动时间为t秒,则△CMN的面积为S关于t函数的图象大致是( )


 如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b>4x+2的解集为x<-1.
如图,直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式kx+b>4x+2的解集为x<-1.