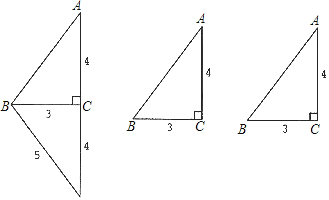题目内容
【题目】在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：
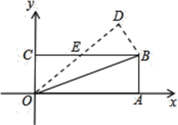
若矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的外延矩形．点A，B，C的所有外延矩形中，面积最小的矩形称为点A，B，C的最佳外延矩形．例如，图中的矩形
，
，
都是点A，B，C的外延矩形，矩形是点A，B，C的最佳外延矩形．
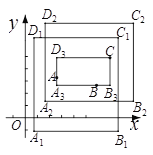
（1）如图1，已知A（－2，0），B（4，3），C（0，
）．
①若
，则点A，B，C的最佳外延矩形的面积为 ；
②若点A，B，C的最佳外延矩形的面积为24，则的值为 ；
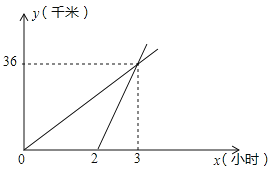
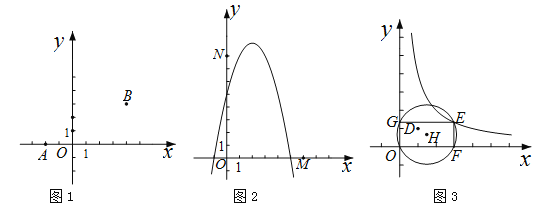
（2）如图2，已知点M（6，0），N（0，8）．P（
，
）是抛物线
上一点，求点M，N，P的最佳外延矩形面积的最小值，以及此时点P的横坐标的取值范围；
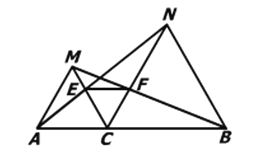
（3）如图3，已知点D（1，1）．E（
，
）是函数
的图象上一点，矩形OFEG是点O，D，E的一个面积最小的最佳外延矩形，⊙H是矩形OFEG的外接圆，请直接写出⊙H的半径r的取值范围．
【答案】（1）①18；②t=4或t=－1；（2）48；
，或
；（3）
【解析】
试题（1）根据给出的新定义进行求解；（2）过M点作
轴的垂线与过N点垂直于
轴的直线交于点Q，则当点P位于矩形OMQN内部或边界时，矩形OMQN是点M，N，P的最佳外延矩形，且面积最小；根据当y=0是y=8时求出x的值得到取值范围；（3）根据最佳外延矩形求出半径的取值范围.
试题解析：（1）①18； ②t=4或t=－1；
（2）如图，过M点作轴的垂线与过N点垂直于轴的直线交于点Q，则当点P位于矩形OMQN内部或边界时，矩形OMQN是点M，N，P的最佳外延矩形，且面积最小．
∵S矩形OMQN＝OM·ON＝6×8＝48， ∴点M，N，P的最佳外延矩形面积的最小值为48．
抛物线
与轴交于点T（0，5）． 令
，有
，
解得：x=－1（舍去），或x=5．
令y=8，有
，解得x=1，或x=3．∴，或．
（3）．
