Question

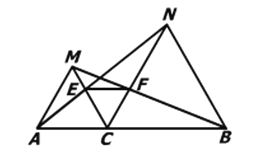
【题目】如图，点C为线段AB上一点，△ACM， △CBN是等边三角形，连结AN，交MC于点E，连结MB交CN于F.

(1)求证：AN=BM；

(2)求证： ∠CEA=∠CFM .

Answer 1

【答案】（1）见详解；（2）见详解.

【解析】

（1）由等边三角形可得其对应线段相等，对应角相等，进而可由SAS得到△ACN≌△MCB，结论得证；

（2）由（1）得△ACN≌△MCB，则∠CBF=∠CNE，由三角形的外角性质，即可得到∠CEA=∠CFM .

证明：如图：

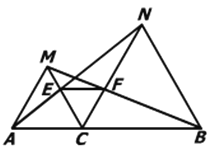
（1）∵△ACM，△CBN是等边三角形，

∴AC=MC，CN=CB，，∠ACM=∠NCB=60°，

∴∠ACM+∠MCN=∠NCB+∠MCN，

即∠ACN=∠MCB，

在△ACN和△MCB中，

，

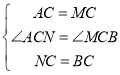∴△ACN≌△MCB（SAS），

∴AN=BM．

（2）由（1）得，△ACN≌△MCB，

∴∠CBF=∠CNE，

∵∠ACM=∠NCB=∠MCN=60°，

∴∠CBF+∠NCB=∠CNE+∠MCN，

∴∠CEA=∠CFM .