题目内容
10. 在△ABC中,∠C=90°,AC=BC=3,D为AB的中点,点P是AB上的一个动点,PE⊥AC于点E,PF⊥BC于点F.
在△ABC中,∠C=90°,AC=BC=3,D为AB的中点,点P是AB上的一个动点,PE⊥AC于点E,PF⊥BC于点F.(1)求证:AE=PE;
(2)求证:DE=DF;
(3)连接EF,EF的最小值是多少?
分析 (1)首先证明∠CAB=45°,∠AEP=90°,从而可得到∠EAP=∠APE,故此AE=EP;
(2)连接CD,由直角三角形斜边上中线的性质可知:CD=AD,然后由等腰三角形三线合一可求得∠DCF=45°,然后由矩形的性质可证得:AE=CF,从而可证明△ADE≌△CDF;
(3)由矩形的性质可知EF=CP,然后由垂线段最短可知CP⊥AB时,CP最短,从而可求得CP的长.
解答 证明:(1)∵∠C=90°,AC=BC,
∴∠CAB=45°,
∵PE⊥AC,
∴∠AEP=90°,
在△AEP中,∠APE=180°-90°-45°=45°,
∴∠EAP=∠APE.
∴AE=EP;
(2)连接CD.
∵∠C=90°,D为AB的中点,
∴CD=AD.
∵AC=BC,D是AB的中点,
∴∠DCF=$\frac{1}{2}$∠ACB=45°.
∴∠A=∠FCD.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=90°,
∴∠ECF=∠PEC=∠PFC=90°.
∴四边形EPCF是矩形.
∴EP=CF
∵AE=PF
∴AE=CF
在△ADE和△CDF中,$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠FCD}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF
∴DE=DF
(3)∵四边形EPCF是矩形
∴EF=CP
∴EF最小时,CP也最小.
由垂线段最短可知:当CP⊥AB时,PC最短.
∴当点P为AB的中点,CP最小.
在Rt△ABC中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}=\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$
∴EF的最小值=CP=$\frac{1}{2}AB=\frac{3\sqrt{2}}{2}$.
点评 本题主要考查的是矩形的性质和判定、求得三角形的性质和判定、直角三角形斜边上中线的性质、等腰三角形的性质,垂线段最短,熟练掌握相关性质是解题的关键.

 如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )
如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )| A. | 主视图 | B. | 俯视图 | C. | 左视图 | D. | 三视图 |
| A. | 10cm | B. | 3cm | C. | 4cm | D. | 5cm |
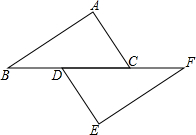 △ABC和△FED中,BD=FC,∠B=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).
△ABC和△FED中,BD=FC,∠B=∠F.当添加条件AB=EF时,就可得到△ABC≌△FED,依据是SAS(只需填写一个你认为正确的条件).