题目内容
 如图,在△ABC中,∠A=50°,AB>AC,D、E分别在AB、AC上,且BD=CE,BE、CD相交于O点,∠BCD=∠EBC,M为BE上一点,∠OCM=∠OBD.
如图,在△ABC中,∠A=50°,AB>AC,D、E分别在AB、AC上,且BD=CE,BE、CD相交于O点,∠BCD=∠EBC,M为BE上一点,∠OCM=∠OBD. (1)求证:CM=CE;
(2)求∠BOC的度数.
考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:(1)先求出∠BCM=∠CBD,然后利用“ASA”证明△BCM和△CBD全等,根据全等三角形对应边相等可得BD=CM,再根据BD=CE即可得证;
(2)设∠ABE=x,∠EBC=y,根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠CEM,再根据等腰三角形的两底角相等表示出∠ECM,然后在△ABC中,利用三角形的内角和定理列式计算求出y,在△OBC中,利用三角形的内角和定理列式进行计算即可得解.
(2)设∠ABE=x,∠EBC=y,根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠CEM,再根据等腰三角形的两底角相等表示出∠ECM,然后在△ABC中,利用三角形的内角和定理列式计算求出y,在△OBC中,利用三角形的内角和定理列式进行计算即可得解.
解答:(1)证明:∵∠BCD=∠EBC,∠OCM=∠OBD,
∴∠BCD+∠OCM=∠EBC+∠OBD,
即∠BCM=∠CBD,
在△BCM和△CBD中,
,
∴△BCM≌△CBD(ASA),
∴BD=CM,
∵BD=CE,
∴CM=CE;
(2)解:设∠ABE=x,∠EBC=y,
∵∠A=50°,
∴∠CEM=∠ABE+∠A=x+50°,
∴∠ECM=180°-2∠CEM=180°-2(x+50°)=80°-2x,
∵∠BCM=∠CBD=x+y,
∴在△ABC中,∠A+∠CBD+∠BCE=180°,
即50°+(x+y)+(x+y+80°-2x)=180°,
整理得,2y=50°,
解得y=25°,
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-25°-25°=130°.
∴∠BCD+∠OCM=∠EBC+∠OBD,
即∠BCM=∠CBD,
在△BCM和△CBD中,
|
∴△BCM≌△CBD(ASA),
∴BD=CM,
∵BD=CE,
∴CM=CE;
(2)解:设∠ABE=x,∠EBC=y,
∵∠A=50°,
∴∠CEM=∠ABE+∠A=x+50°,
∴∠ECM=180°-2∠CEM=180°-2(x+50°)=80°-2x,
∵∠BCM=∠CBD=x+y,
∴在△ABC中,∠A+∠CBD+∠BCE=180°,
即50°+(x+y)+(x+y+80°-2x)=180°,
整理得,2y=50°,
解得y=25°,
在△OBC中,∠BOC=180°-∠OBC-∠OCB=180°-25°-25°=130°.
点评:本题考查了全等三角形的判定,等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,(2)解法巧妙,利用三角形内角和定理列式正好消掉x.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
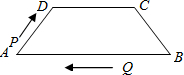 在等腰梯形ABCD中,AB∥DC,AD=BC=6cm,DC=7cm,AB=12cm,点P从点A出发,以每秒3cm的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒2cm的速度沿BA向终点A运动.在运动期间,当四边形AQPD为平行四边形时,运动时间为( )
在等腰梯形ABCD中,AB∥DC,AD=BC=6cm,DC=7cm,AB=12cm,点P从点A出发,以每秒3cm的速度沿AD→DC向终点C运动,同时点Q从点B出发,以每秒2cm的速度沿BA向终点A运动.在运动期间,当四边形AQPD为平行四边形时,运动时间为( )| A、3.6秒 | B、4秒 |
| C、4.4秒 | D、4.8秒 |
掷一枚硬币三次,其中有两次正面朝上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:如图,在等边△ABC中,点D为AC上任意一点,且∠EDF=60°.
已知:如图,在等边△ABC中,点D为AC上任意一点,且∠EDF=60°. 某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,甲车途经配货站C,并在C地用1小时配货,然后按原速开往B地,乙车从B地经C站直达A地.如图是甲、乙两车间的距离y(千米)与乙车出发时间x(时)的函数的部分图象,则B、C两地间的距离是
某物流公司的甲、乙两辆货车分别从A、B两地同时相向而行,并以各自的速度匀速行驶,甲车途经配货站C,并在C地用1小时配货,然后按原速开往B地,乙车从B地经C站直达A地.如图是甲、乙两车间的距离y(千米)与乙车出发时间x(时)的函数的部分图象,则B、C两地间的距离是