题目内容
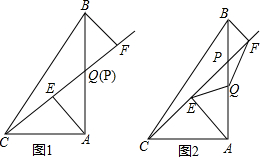
12.已知,在Rt△ABC中,∠A=90°,点P是直角边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F、Q为AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系式EQ=FQ;
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.
分析 (1)根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;
(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可;
解答 解:(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,
理由是:∵Q为AB的中点,
∴AQ=BQ,
∵AE⊥CQ,BF⊥CQ,
∴AE∥BF,∠AEQ=∠BFQ=90°,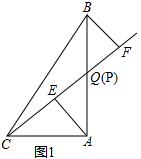
在△AEQ和△BFQ中,
$\left\{\begin{array}{l}{∠AQE=∠BQF}\\{∠AEQ=∠BFQ}\\{AQ=BQ}\end{array}\right.$,
∴△AEQ≌△BFQ,
∴EQ=FQ,
故答案为:AE∥BF,EQ=FQ;
(2)QE=QF,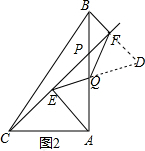
证明:如图2,延长EQ交BF于D,
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
在△AEQ和△BDQ中,
$\left\{\begin{array}{l}{∠AQE=∠BQD}\\{∠AEQ=∠BDQ}\\{AQ=BQ}\end{array}\right.$,
∴△AEQ≌△BDQ,
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF.
点评 本题考查了平行线的性质和判定,全等三角形的性质和判定,直角三角形的性质的应用,解此题的关键是求出△AEQ≌△BDQ,用了运动观点,难度适中.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
2. 如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
 如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O-C-D-O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )| A. | 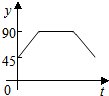 | B. | 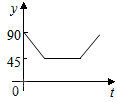 | C. | 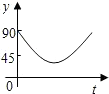 | D. | 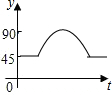 |
17. 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
 如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )
如图,边长为a,b的矩形的周长为14,面积为10,则a2b+ab2的值为( )| A. | 140 | B. | 70 | C. | 35 | D. | 24 |
1.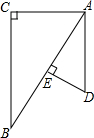 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
 如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )
如图,已知△ABC与△ADE中,∠C=∠AED=90°,点E在AB上,那么添加下列一个条件后,仍无法判定△ABC∽△DAE的是( )| A. | $\frac{AC}{DE}$=$\frac{AB}{AD}$ | B. | ∠B=∠D | C. | AD∥BC | D. | ∠BAC=∠D |
2.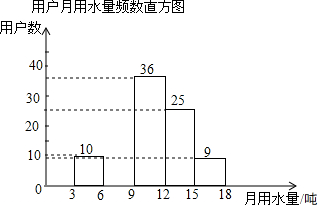 水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
 水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:
水利部确定每年的3月22日至28日为“中国水周”(1994年以前为7月1日至7日),从1991年起,我国还将每年5月的第二周作为城市节约用水宣传周.某社区为了进一步提高居民珍惜水、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每月的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图表:| 用户月用水量频数分布表 | ||
| 平均用水量(吨) | 频数 | 频率 |
| 3~6吨 | 10 | 0.1 |
| 6~9吨 | m | 0.2 |
| 9~12吨 | 36 | 0.36 |
| 12~15吨 | 25 | n |
| 15~18吨 | 9 | 0.09 |
(1)在频数分布表中:m=20,n=0.25;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
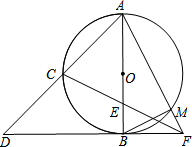 如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.
如图,AB是⊙O的直径,C是$\widehat{AB}$的中点,延长AC至点D,使AC=CD,DB的延长线交CE的延长线于点F,AF交⊙O于点M,连接BM.