题目内容
20.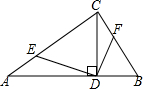 如图,△ABC中,∠ACB=90°,CD⊥AB于D,E、F分别为AC、BC上一点,且DE⊥DF,若∠A=30°,求$\frac{DF}{DE}$的值.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,E、F分别为AC、BC上一点,且DE⊥DF,若∠A=30°,求$\frac{DF}{DE}$的值.
分析 由Rt△ABC中,CD⊥AB,得出∠FCD=∠A,利用互余关系得出∠CDF=∠ADE,证明△ADE∽△CDF,利用相似比证明结论.
解答 证明:∵∠ACB=90°CD⊥AB,
∴∠FCD+∠ACD=∠A+∠ACD=90°,
∴∠FCD=∠A,
同理可证∠CDF=∠ADE,
∴△ADE∽△CDF,
∴$\frac{DF}{DE}=\frac{DC}{AD}$,
∵∠A=30°,
∴tan∠A=$\frac{CD}{AD}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{DF}{DE}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了相似三角形的判定与性质.关键是利用互余关系证明角相等,再证明三角形相似.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
8.下列事件中,是不可能事件的是( )
| A. | 买一张电影票,座位号是偶数 | B. | 度量三角形的内角和,结果是360° | ||
| C. | 明天会下雨 | D. | 设计运动员射击一次,命中8环 |
10. 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
 如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )
如图,在正方形ABCD内作等边△AED,连接AC,则∠EAC的度数为( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
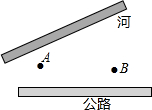 如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.
如图,公路与大河的中间地带有两个工厂A,B,现要在公路上建一仓库,在河边修一水泵站.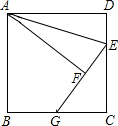 如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.
如图,正方形ABCD中,点E在边CD上,将△ADE沿AE翻折至△AFE,延长EF交边BC于点G,若点E是CD中点,则BG:CG=1:2.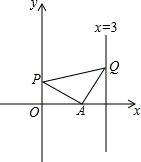 如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
如图,在平面直角坐标系xOy中,点A的坐标为(2,0),Q是直线x=3上的一个动点,y轴正半轴上是否存在点P,使△APQ为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.