题目内容
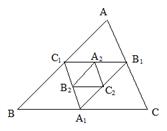
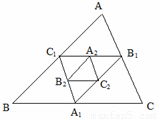
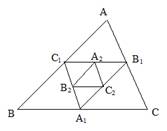
如图，点A1、B1、C1分别是△ABC的三边BC、AC、AB的中点， 点A2、B2、C2分别是△A1B1C1的边B1C1、A1C1、A1B1的中点，依此 类推，则△AnBnCn与△ABC的面积比为 ▲ ．
【答案】
【解析】解：设△ABC的面积为1，
∵A1、B1、C1分别是△ABC的边BC、CA、AB的中点，
∴A1B1、A1C1、B1C1是△ABC的中位线，
∴△
∽△ABC，且相似比为
∴
：
=1：4，且S△ABC=1
∴=
．
∵A2、B2、C2分别是
的边
、
、
的中点，
∴∽
且相似比为
∴S△A2B2C2=
．依次类推
∴S△A3B3C3=
…
∴S△AnBnCn= ．
故答案为：
练习册系列答案
相关题目
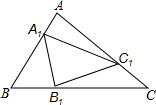附加题：如图，点A1，B1，C1分别在△ABC的边AB，BC，CA上，且
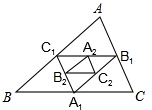（2012•六合区一模）如图，点A1、B1、C1分别是△ABC的三边BC、AC、AB的中点，点A2、B2、C2分别是△A1B1C1的边B1C1、A1C1、A1B1的中点，依此类推，则△AnBnCn与△ABC的面积比为
