题目内容
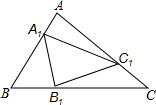 附加题:如图,点A1,B1,C1分别在△ABC的边AB,BC,CA上,且
附加题:如图,点A1,B1,C1分别在△ABC的边AB,BC,CA上,且| AA1 |
| AB |
| BB1 |
| BC |
| CC1 |
| CA |
| 1 |
| 2 |
分析:过B1作AC的平行线交AB于A2,根据平行线分线段成比例定理,表示出B1A2、A1A2,再根据三角形两边之和大于第三边,A1B1<(1-2k)AB+kAC,同理可得B1C1<(1-2k)BC+kAB,A1C1<(1-2k)AC+kBC,然后根据三角形周长定义计算即可.
解答: 证明:如图,过B1作AC的平行线交AB于A2,
证明:如图,过B1作AC的平行线交AB于A2,
则有
=
=
=k,
∴A2B1=kAC,BA2=kAB,
∵AA1=kAB,
∴A1A2=AB-AA1-BA2=(1-2k)AB,
在△A1A2B1中,A1B1<A1A2+B1A2=(1-2k)AB+kAC,
同理可得B1C1<(1-2k)BC+kAB,A1C1<(1-2k)AC+kBC,
∴A1B1+B1C1+A1C1<(1-2k)AB+kAC+(1-2k)BC+kAB+(1-2k)AC+kBC
整理得A1B1+B1C1+A1C1<(1-k)(AB+BC+CA),
即p1<(1-k)p.
 证明:如图,过B1作AC的平行线交AB于A2,
证明:如图,过B1作AC的平行线交AB于A2,则有
| BB1 |
| BC |
| A2B1 |
| AC |
| BA2 |
| AB |
∴A2B1=kAC,BA2=kAB,
∵AA1=kAB,
∴A1A2=AB-AA1-BA2=(1-2k)AB,
在△A1A2B1中,A1B1<A1A2+B1A2=(1-2k)AB+kAC,
同理可得B1C1<(1-2k)BC+kAB,A1C1<(1-2k)AC+kBC,
∴A1B1+B1C1+A1C1<(1-2k)AB+kAC+(1-2k)BC+kAB+(1-2k)AC+kBC
整理得A1B1+B1C1+A1C1<(1-k)(AB+BC+CA),
即p1<(1-k)p.
点评:本题主要利用三角形的两边之和大于第三边的性质和平行线分线段成比例定理,熟练掌握性质和定理是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 附加题:如图,点A1,B1,C1分别在△ABC的边AB,BC,CA上,且
附加题:如图,点A1,B1,C1分别在△ABC的边AB,BC,CA上,且 ,若△ABC的周长为p,△A1B1C1的周长为p1;求证:p1<(1-k)p.
,若△ABC的周长为p,△A1B1C1的周长为p1;求证:p1<(1-k)p. ,若△ABC的周长为p,△A1B1C1的周长为p1;求证:p1<(1-k)p.
,若△ABC的周长为p,△A1B1C1的周长为p1;求证:p1<(1-k)p.

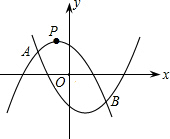
 ,且与抛物线y2=ax2-ax-1相交于A,B两点.设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤x≤xB,过q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
,且与抛物线y2=ax2-ax-1相交于A,B两点.设A,B两点的横坐标分别记为xA,xB,若在x轴上有一动点Q(x,0),且xA≤x≤xB,过q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?