题目内容
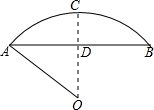 如图,某座桥的桥拱是圆弧形,它的跨度AB为8米,拱高CD为2米,求桥拱的半径.
如图,某座桥的桥拱是圆弧形,它的跨度AB为8米,拱高CD为2米,求桥拱的半径.考点:垂径定理的应用,勾股定理
专题:
分析:设圆的半径为R米,由于CD平分弧AB,且CD⊥AB,根据垂径定理的推论得到圆心O在CD的延长线上,再根据垂径定理得到CD平分AB,则AD=
AB=4,在Rt△OAD中,利用勾股定理可计算出半径R.
| 1 |
| 2 |
解答:解:设圆的半径为R米,
∵CD平分弧AB,且CD⊥AB,
∴圆心O在CD的延长线上,
∴CD平分AB,
∴AD=
AB=4,
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-2,
∵OA2=OD2+AD2,
∴R2=42+(R-2)2,
解得R=5,
即桥拱所在圆的半径5米.
∵CD平分弧AB,且CD⊥AB,
∴圆心O在CD的延长线上,
∴CD平分AB,
∴AD=
| 1 |
| 2 |
在Rt△OAD中,AD=6,OA=R,OD=R-CD=R-2,
∵OA2=OD2+AD2,
∴R2=42+(R-2)2,
解得R=5,
即桥拱所在圆的半径5米.
点评:本题考查了垂径定理的应用:先把实际问题中的数据与几何图形中的量对应起来,然后根据垂径定理及其推论进行证明或计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数:①y=2x;②y=-3x+2;③y=
(x<0);④y=-x2+2x+3,其中y的值随x值的增大而减小的函数有( )
| 2 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
在抛物线y=x2-4x-4上的一个点是( )
| A、(4,4) | ||||
| B、(3,-1) | ||||
| C、(-2,-8) | ||||
D、(-
|
 如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )| A、35° | B、45° |
| C、55° | D、65° |
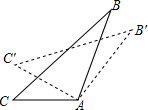 如图,△AB′C′是由△ABC绕顶点A按顺时针方向旋转后得到的,已知∠B=30°,∠C=40°.试探究:
如图,△AB′C′是由△ABC绕顶点A按顺时针方向旋转后得到的,已知∠B=30°,∠C=40°.试探究: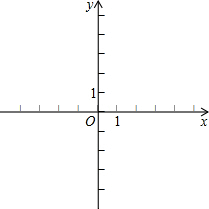 在所给平面直角坐标系中描点、画图:
在所给平面直角坐标系中描点、画图: 如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢?
如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢?