题目内容
13. 如图,菱形ABCD中,AB=6,∠BCD=120°,
如图,菱形ABCD中,AB=6,∠BCD=120°,(1)过点A作AE垂直BC于E.
(2)求菱形ABCD的面积.
分析 (1)作△ABC边BC上的高即可.
(2)根据菱形的性质得BC=AB=6,AB∥CD,则利用互补得到∠B=180°-∠BCD=60°,在Rt△ABE中,由于∠BAE=90°-∠B=30°,则BE=$\frac{1}{2}$AB=3,于是可根据勾股定理计算出AE=3$\sqrt{3}$,然后根据平行四边形的面积公式计算菱形ABCD的面积.
解答 解:(1)如图,AE为所作;
(2)∵四边形ABCD是菱形,
∴BC=AB=6,AB∥CD,
∴∠B+∠BCD=180°,
∴∠B=180°-∠BCD=180°-120°=60°,
∵AE⊥BC,
∴∠BAE=90°-∠B=30°,
∴BE=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
在Rt△ABE中,AE=$\sqrt{{{6}^{2}-3}^{2}}$=3$\sqrt{3}$,
∴菱形ABCD的面积=AE•BC=3$\sqrt{3}$×6=18$\sqrt{3}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形的面积等于对角线乘积的一半.

练习册系列答案
相关题目
3.若a的倒数是2,则a的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
4. 如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内填入适当的数,使它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C的三个数依次为( )
如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内填入适当的数,使它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C的三个数依次为( )
 如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内填入适当的数,使它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C的三个数依次为( )
如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内填入适当的数,使它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A,B,C的三个数依次为( )| A. | -2,-3,-1 | B. | -3,-1,-2 | C. | -1,-2,-3 | D. | -1,-3,-2 |
8.一元二次方程x2+5=-4x的一次项的系数是( )
| A. | 4 | B. | -4 | C. | 1 | D. | 5 |
18. 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,DE=4cm,则BC的长为( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,DE=4cm,则BC的长为( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,DE=4cm,则BC的长为( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}=\frac{1}{2}$,DE=4cm,则BC的长为( )| A. | 8cm | B. | 12cm | C. | 11cm | D. | 10cm |
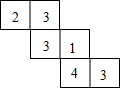 一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图.
一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图.