Question

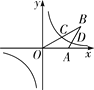
【题目】如图，正六边形的对称中心在反比例函数（，）的图象上，边在轴上，点在轴上，已知．

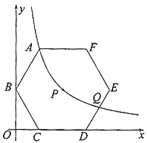
（1）点是否在该反比例函数的图象上？请说明理由；

（2）若该反比例函数图象与交于点，求点的横坐标；

（3）平移正六边形，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．

Answer 1

【答案】（1）点在该反比例函数的图像上，理由见解析；（2）；（3）答案见解析．

【解析】

（1）过点P作x轴垂线PH，连接PC，可得PC=4，C是OH的中点，所以；

（2）易求D（6，0），设，则，求得代入反比例函数解析式求得b的值即可得解；

（3）求得正六边形各顶点坐标，根据平移性质即可得其一边的两个端点恰好都落在该反比例函数的图象上．

（1）如图，连结，过点作轴于点，

∵在正六边形中，点在轴上，

∴和都是含有角的直角三角形，

，

∴，，

∴，

又∵点在反比例函数上，

∴反比例函数解析式为：（），

连结，过点作于点，

∵，，

∴，，，

∴，

∴点在该反比例函数的图像上．

（2）过点作轴于点，

∵六边形为正六边形，

∴，

设，则，

∴，

又∵点在反比例函数上，

∴，

解得：，（舍去），

∴，

∴点的横坐标为

（3）易求A（2，4），B（0，2），C（2，0），D（6，0），E（8，2），F（6，4），

设正六边形向左平移m个单位，向上平移n个单位，则平移后点的坐标分别为

∴A（2-m，4+n），B（-m，2+n），C（2-m，n），D（6-m，n），E（8-m，2+n），F（6-m，2+n），

①将正六边形向左平移4个单位后，E（4，2），F（2，4），则点E与F都在反比例函数图象上；

②将正六边形向右平移2个单位，再向上平移2个单位后，C（4，2），B（2，4），则点B与C都在反比例函数图象上．