题目内容
17.计算:(1)(2$\sqrt{3}-\sqrt{6}$)×$\sqrt{12}$;
(2)($\sqrt{48}-\sqrt{27}+$4$\sqrt{15}$)÷3;
(3)(2$\sqrt{3}$-5$\sqrt{2}$)($\sqrt{3}$-2$\sqrt{2}$);
(4)(2$\sqrt{3}$+3$\sqrt{2}$)(2$\sqrt{3}$-3$\sqrt{2}$);
(5)(2$\sqrt{3}$-1)2;
(6)($\frac{\sqrt{5}+1}{2}$)2+($\frac{\sqrt{5}-1}{2}$)2;
(7)($\frac{2-\sqrt{3}}{2}$)2-($\frac{2+\sqrt{3}}{2}$)2;
(8)(3+2$\sqrt{5}$)2-(4+$\sqrt{7}$)(4-$\sqrt{7}$);
(9)$\frac{3}{2}$$\sqrt{20}$•(-$\frac{1}{3}$$\sqrt{48}$);
(10)$\sqrt{\frac{24}{5}}$×3$\sqrt{5}$÷$\sqrt{6}$;
(11)$\sqrt{50}$-$\frac{1}{\sqrt{5}}$+2$\sqrt{20}$-$\sqrt{45}$+$\sqrt{\frac{1}{2}}$.
分析 (1)利用二次根式的乘法法则运算;
(2)先把二次根式化为最简二次根式,然后合并后进行除法运算;
(3)利用多项式乘法展开,然后合并即可;
(4)根据平方差公式计算;
(5)根据完全平方公式计算;
(6)根据完全平方公式计算;
(7)利用平方差公式计算;
(8)根据完全平方公式和平方差公式计算;
(9)利用二次根式的乘法法则运算;
(10)利用二次根式的乘除法则运算;
(11)先把二次根式化为最简二次根式,然后合并即可.
解答 解:(1)原式=2$\sqrt{3×12}$-$\sqrt{6×12}$=12-6$\sqrt{2}$;
(2)原式=(4$\sqrt{3}$-3$\sqrt{3}$+4$\sqrt{15}$)÷3=$\frac{\sqrt{3}}{3}$+$\frac{4\sqrt{15}}{3}$;
(3)原式=6-4$\sqrt{6}$-5$\sqrt{6}$+20=26-9$\sqrt{6}$;
(4)原式=12-18=-6;
(5)原式=12-4$\sqrt{3}$+1=13-4$\sqrt{3}$;
(6)原式=$\frac{5+2\sqrt{5}+1}{4}$+$\frac{5-2\sqrt{5}+1}{4}$=3;
(7)原式=($\frac{2-\sqrt{3}}{2}$+$\frac{2+\sqrt{3}}{2}$)($\frac{2-\sqrt{3}}{2}$-$\frac{2+\sqrt{3}}{2}$)=2×(-$\sqrt{3}$)=-2$\sqrt{3}$;
(8)原式=9+12$\sqrt{5}$+20-(16-7)=29+12$\sqrt{5}$-9=20+12$\sqrt{5}$;
(9)原式=3$\sqrt{5}$×(-$\frac{4\sqrt{3}}{3}$)=-4$\sqrt{15}$;
(10)原式=3$\sqrt{\frac{24}{5}×5×\frac{1}{6}}$=6;
(11)原式=5$\sqrt{2}$-$\frac{\sqrt{5}}{5}$+4$\sqrt{5}$-3$\sqrt{5}$+$\frac{\sqrt{2}}{2}$=$\frac{11\sqrt{2}}{2}$+$\frac{4\sqrt{5}}{5}$.
点评 本题考查了二次根式的混合运算:在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

| A. | $\sqrt{25}$=±5 | B. | ±$\sqrt{25}$=5 | C. | $\sqrt{{({-5})}^2}$=5 | D. | $\sqrt{{({-3})}^2}$=-3 |
| A. | 5 | B. | 8 | C. | 10 | D. | 17 |
 如图,阳光下斜坡旁有一棵树AB,它的阴影投在斜坡上为AC=10米,斜坡与平面形成的坡角∠DAC=15°,光线与斜坡形成的∠BCA=75°.求树AB的高度(精确到0.1米)参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,$\sqrt{3}$≈1.73.
如图,阳光下斜坡旁有一棵树AB,它的阴影投在斜坡上为AC=10米,斜坡与平面形成的坡角∠DAC=15°,光线与斜坡形成的∠BCA=75°.求树AB的高度(精确到0.1米)参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,$\sqrt{3}$≈1.73.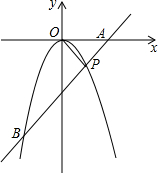 如图,抛物线y=ax2(a≠0)与直线AB交于点P(4,-4),连接OP,则OP=AP,求二次函数的解析式及抛物线与直线AB另一个交点B的坐标.
如图,抛物线y=ax2(a≠0)与直线AB交于点P(4,-4),连接OP,则OP=AP,求二次函数的解析式及抛物线与直线AB另一个交点B的坐标.