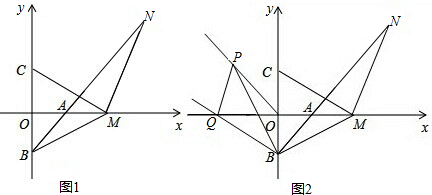
题目内容
如图1,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足a2-8a+16+
=0,点C、B关于x轴对称.
(1)求A、C两点坐标.
(2)点M为射线OA上A点右侧一动点,过点M作MN⊥CM交直线AB于N,连接BM,是否存在点M,使S△AMN=
S△AMB?若存在,求点M的坐标;若不存在,说明理由.
(3)如图2,点P为第二象限角平分线上一动点,将射线BP绕点B逆时针旋转30°交x轴于Q,连接PQ,在点P运动过程中,当∠BPQ=45°时,求BQ的长.
| b+4 |
(1)求A、C两点坐标.
(2)点M为射线OA上A点右侧一动点,过点M作MN⊥CM交直线AB于N,连接BM,是否存在点M,使S△AMN=
| 3 |
| 2 |
(3)如图2,点P为第二象限角平分线上一动点,将射线BP绕点B逆时针旋转30°交x轴于Q,连接PQ,在点P运动过程中,当∠BPQ=45°时,求BQ的长.

考点:几何变换综合题
专题:
分析:(1)由a,b满足a2-8a+16+
=0,可求得a与b的值,即可求得A、B两点坐标,又由点C,B关于x轴对称,即可求得C的坐标;
(2)首先连接AC,易得AB=AC,MB=MC,可得∠MBA=∠MCA,继而证得MN=MB=MC,然后过点N作NE⊥x轴于E,可证得△OCM≌△EMN,再设AM=x,NE=4+x,由S△AMN=
S△AMB,即可求得答案;
(3)首先过P作PM⊥y轴于M,PN⊥x轴于N,PH⊥PQ交y轴于H,易证得△PQN≌△PHM,继而可证得△QPB≌△HPB,则可求得∠OBP=∠PBQ=30°,继而可得∠BQO=30°,继而求得答案.
| b+4 |
(2)首先连接AC,易得AB=AC,MB=MC,可得∠MBA=∠MCA,继而证得MN=MB=MC,然后过点N作NE⊥x轴于E,可证得△OCM≌△EMN,再设AM=x,NE=4+x,由S△AMN=
| 3 |
| 2 |
(3)首先过P作PM⊥y轴于M,PN⊥x轴于N,PH⊥PQ交y轴于H,易证得△PQN≌△PHM,继而可证得△QPB≌△HPB,则可求得∠OBP=∠PBQ=30°,继而可得∠BQO=30°,继而求得答案.
解答:解:(1)∵a、b满足a2-8a+16+
=0,
即a,b满足(a-4)2+
=0,
∴a-4=0,b+4=0,
解得:a=4,b=-4,
∴A(4,0),B(0,-4),
∵C,B关于x轴对称,
∴C(0,4);
(2)连接AC,
∵点C,B关于x轴对称,
∴OM垂直平分BC,
∴AB=AC,MB=MC,
∴∠ACB=∠ABC,∠MCB=∠MBC,
∴∠MBA=∠MCA,
∵∠CAN=90゜=∠CMN,
∴∠MCA=∠ANM=∠MBA,
∴MN=MB=MC,
过点N作NE⊥x轴于E,
∵∠OMC+∠EMN=90°,∠OCM+∠OMC=90°,
∴∠OCM=∠EMN,
在△OCM和△EMN中,
,
∴△OCM≌△EMN(AAS),
∴NE=OM,
设AM=x,NE=4+x,
∵S△AMN:S△AMB=3:2,
∴
=
,
解得:x=2,
∴OM=NE=6,
∴M(6,0).
(3)过P作PM⊥y轴于M,PN⊥x轴于N,PH⊥PQ交y轴于H,
∵∠QPN+∠NPH=90°,∠MPH+∠NPH=90°,
∴∠QPN=∠MPH,
 又∵PO平分∠MOQ,
又∵PO平分∠MOQ,
∴PM=PN,
在△PQN和△PHM中,
,
∴△PQN≌△PHM(ASA),
∴PQ=PH,
又∵∠BPQ=45°,∠QPH=90°,
∴∠BPH=45°,
在△QPB和△HPB中,
,
∴△QPB≌△HPB(SAS),
∴∠PBO=∠PBQ=30°,
∴∠OBQ=∠PBO+∠PBQ=60°,
∴∠OQB=90°-∠OBQ=30°,
∴在Rt△QOB中,OB=
QB,
又∵OB=4,
∴BQ=8.
| b+4 |
即a,b满足(a-4)2+
| b+4 |
∴a-4=0,b+4=0,
解得:a=4,b=-4,
∴A(4,0),B(0,-4),
∵C,B关于x轴对称,
∴C(0,4);
(2)连接AC,
∵点C,B关于x轴对称,
∴OM垂直平分BC,

∴AB=AC,MB=MC,
∴∠ACB=∠ABC,∠MCB=∠MBC,
∴∠MBA=∠MCA,
∵∠CAN=90゜=∠CMN,
∴∠MCA=∠ANM=∠MBA,
∴MN=MB=MC,
过点N作NE⊥x轴于E,
∵∠OMC+∠EMN=90°,∠OCM+∠OMC=90°,
∴∠OCM=∠EMN,
在△OCM和△EMN中,
|
∴△OCM≌△EMN(AAS),
∴NE=OM,
设AM=x,NE=4+x,
∵S△AMN:S△AMB=3:2,
∴
| x+4 |
| 4 |
| 3 |
| 2 |
解得:x=2,
∴OM=NE=6,
∴M(6,0).
(3)过P作PM⊥y轴于M,PN⊥x轴于N,PH⊥PQ交y轴于H,
∵∠QPN+∠NPH=90°,∠MPH+∠NPH=90°,
∴∠QPN=∠MPH,
 又∵PO平分∠MOQ,
又∵PO平分∠MOQ,∴PM=PN,
在△PQN和△PHM中,
|
∴△PQN≌△PHM(ASA),
∴PQ=PH,
又∵∠BPQ=45°,∠QPH=90°,
∴∠BPH=45°,
在△QPB和△HPB中,
|
∴△QPB≌△HPB(SAS),
∴∠PBO=∠PBQ=30°,
∴∠OBQ=∠PBO+∠PBQ=60°,
∴∠OQB=90°-∠OBQ=30°,
∴在Rt△QOB中,OB=
| 1 |
| 2 |
又∵OB=4,
∴BQ=8.
点评:此题考查了全等三角形的判定与性质、线段垂直平分线的性质、等腰三角形的判定与性质以及非负性.此题难度较大,注意掌握辅助线的作法,注意数形结合与方程思想的应用.

练习册系列答案
相关题目
已知x、y互为倒数,m、n互为相反数,则(-xy)2011-(m+n)2011的值( )
| A、1 | B、-1 | C、0 | D、-2 |
△ABC中,A、B两点坐标分别是(0,0)和(36,15),点C的横、纵坐标均为整数,则△ABC的面积的最小值是( )
A、
| ||
| B、1 | ||
C、
| ||
| D、不存在最小值 |
 如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=
如图,已知△ABC≌△CDA,A和C,D和B分别是对应点,如果AB=7cm,AD=6cm,AC=4cm,则DC的长为( )
| A、6cm | B、7cm |
| C、4cm | D、不确定 |
 如图,直线a、b相交于点O,若∠1=40°,则∠2的度数为
如图,直线a、b相交于点O,若∠1=40°,则∠2的度数为