题目内容
生活,是数学的源泉.人们常说,数学抽象、枯燥、难学,其实,数学一旦回到“娘家”,那绚丽多彩的生活就会使她变得生动活泼,非常迷人.今天的世界,科技日新月异,生活丰富多彩,生活中新的数学问题如雨后春笋,不断涌现,学好这类应用问题,对于我们明确学习目的,培养学习兴趣,增强学习动力,提高分析问题和解决问题的能力具有重要的意义.下面就让我们选择例子来共同欣赏.
例:实际测试表明1千克重的干衣物,用水洗涤拧干,湿重为2千克.今用溶质质量分数为1%(提示:溶质质量分数=
×100%,洗衣粉溶液中溶质为洗衣粉,溶液为洗衣粉加水)的洗衣粉溶液洗涤0.5千克的干衣物,然后用总质量为20千克的清水分两次漂洗.假设在洗涤和漂洗的过程中,残留在衣物中的溶液溶质质量分数和它所在的溶液溶质质量分数相等,且每次洗涤、漂洗后都需拧干再进入下一道操作.问怎样分配这20千克清水的用量,可以使残留在衣物上的洗衣粉溶液溶质质量分数最小?残留在衣物上的洗衣粉有多少毫克?(保留3个有效数字)
例:实际测试表明1千克重的干衣物,用水洗涤拧干,湿重为2千克.今用溶质质量分数为1%(提示:溶质质量分数=
| 溶质质量 |
| 溶液质量 |
考点:分式的混合运算
专题:应用题
分析:根据:溶液浓度=溶质质量分数=
×100%,×100%,设第一次放水量为x千克,则溶质的质量=(1-0.5)×1%,溶液的质量=x+0.5,算出第一次残留浓度,第二次残留浓度就是在第一次残留浓度的基础上,在乘以一次浓度,即此时溶质的质量=
×0.5,溶液的质量=20-x+0.5.
| 溶质质量 |
| 溶液质量 |
| 0.5×1% |
| x+0.5 |
解答:解:设第一次放水量为x千克,
则第一次残留浓度=
,
第二次残留浓度=第一次残留浓度×
=
×
=
(这个式子一定要看懂),
求第二次残留浓度最小,
有最小值,
当(x+0.5)(20-x+0.5)有最大值时,第二次残留浓度最小,
∵(x+0.5)(20-x+0.5)=-x2+20x+10.25,
∴当x=10时,(x+0.5)(20-x+0.5)最大,
残留洗衣粉=
×0.5×106≈11.3mg.
则第一次残留浓度=
| 0.5×1% |
| x+0.5 |
第二次残留浓度=第一次残留浓度×
| 0.5 |
| 20-x+0.5 |
| 0.5×1% |
| x+0.5 |
| 0.5 |
| 20-x+0.5 |
| 0.0025 |
| (x+0.5)(20-x+0.5) |
求第二次残留浓度最小,
| 0.0025 |
| (x+0.5)(20-x+0.5) |
当(x+0.5)(20-x+0.5)有最大值时,第二次残留浓度最小,
∵(x+0.5)(20-x+0.5)=-x2+20x+10.25,
∴当x=10时,(x+0.5)(20-x+0.5)最大,
残留洗衣粉=
| 0.0025 |
| (x+0.5)(20-x+0.5) |
点评:本题考查了溶液浓度问题,需要分清楚每一次溶质的质量,溶液的质量;列出计算公式,根据公式求最小值.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,△ABC的三个顶点A、B、C在正方形网格中,每小方格的边长都为
如图,△ABC的三个顶点A、B、C在正方形网格中,每小方格的边长都为
 在同一平面直角坐标系中,画出下列函数的图象.
在同一平面直角坐标系中,画出下列函数的图象.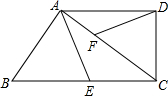 如图,已知在直角梯形ABCD中,∠ADC=90°,AD平行BC,AD=8,DC=6,点E在BC上,点F在AC上,且∠DFC=∠AEB,AF=4.
如图,已知在直角梯形ABCD中,∠ADC=90°,AD平行BC,AD=8,DC=6,点E在BC上,点F在AC上,且∠DFC=∠AEB,AF=4.