题目内容
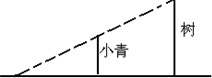一天，小青在校园内发现：旁边一颗树在阳光下的影子和她本人的影子在同一直线上，树顶的影子和她头顶的影子恰好落在地面的同一点，同时还发现她站立于树影的中点（如图所示）．如果小青的身高为1.60米，由此可推断出树高是考点：三角形中位线定理
专题：应用题
分析：根据三角形的中位线定理的数量关系“三角形的中位线等于第三边的一半”，进行计算．
解答：
解：根据题意，知ED=1.60米，ED∥BC，点D是AB的中点．
则DE是△ABC的中位线，
所以，ED=
BC，即BC=2ED=3.20米．
故答案是：3.20．
解：根据题意，知ED=1.60米，ED∥BC，点D是AB的中点．则DE是△ABC的中位线，
所以，ED=
| 1 |
| 2 |
故答案是：3.20．
点评：本题考查运用三角形的中位线定理解决生活中的实际问题，将生活中的实际问题转化为数学问题是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图，在Rt△ABC中，∠ABC=90°，BA=BC．点D是AB的中点，连接CD，过点B作BG丄CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连接DF．给出以下四个结论：①
商城义乌江的两岸绿树葱茏、生机勃勃，成为我市一道亮丽的风景．如图，从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°，测得BC=100如图所示下列几何体中，俯视图形状相同的是（ ）
| A、①④ | B、②③ |
| C、①②④ | D、②③④ |
将抛物线y=-x2向右平移2个单位后的抛物线的解析式是（ ）
| A、y=-（x-2）2 |
| B、y=-（x+2）2 |
| C、y=-x2-2 |
| D、y=-x2+2 |
已知O1和O2的直径分别为6cm和8cm，圆心距O1O2=14cm，则两圆的位置关系为（ ）
| A、相切 | B、内含 | C、外离 | D、相交 |